Gradient-flow adaptive importance sampling for Bayesian leave one out cross-validation for sigmoidal classification models

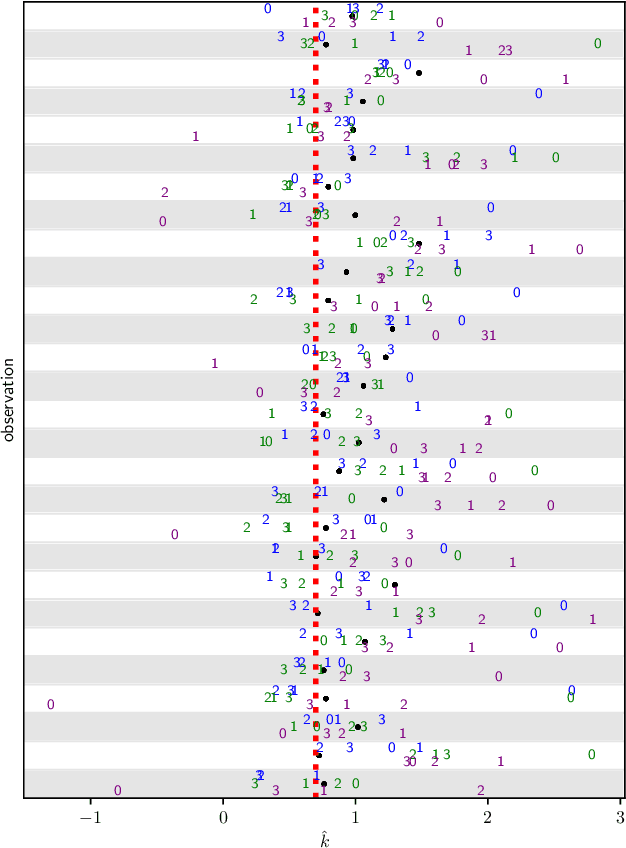
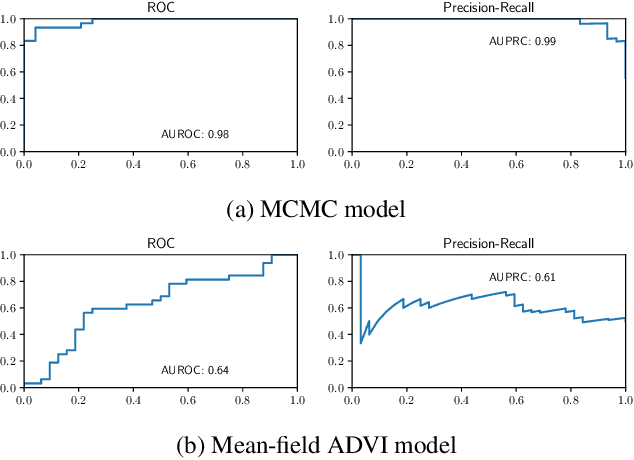
We introduce a set of gradient-flow-guided adaptive importance sampling (IS) transformations to stabilize Monte-Carlo approximations of point-wise leave one out cross-validated (LOO) predictions for Bayesian classification models. One can leverage this methodology for assessing model generalizability by for instance computing a LOO analogue to the AIC or computing LOO ROC/PRC curves and derived metrics like the AUROC and AUPRC. By the calculus of variations and gradient flow, we derive two simple nonlinear single-step transformations that utilize gradient information to shift a model's pre-trained full-data posterior closer to the target LOO posterior predictive distributions. In doing so, the transformations stabilize importance weights. Because the transformations involve the gradient of the likelihood function, the resulting Monte Carlo integral depends on Jacobian determinants with respect to the model Hessian. We derive closed-form exact formulae for these Jacobian determinants in the cases of logistic regression and shallow ReLU-activated artificial neural networks, and provide a simple approximation that sidesteps the need to compute full Hessian matrices and their spectra. We test the methodology on an $n\ll p$ dataset that is known to produce unstable LOO IS weights.

Learning recurrent dynamics in spiking networks

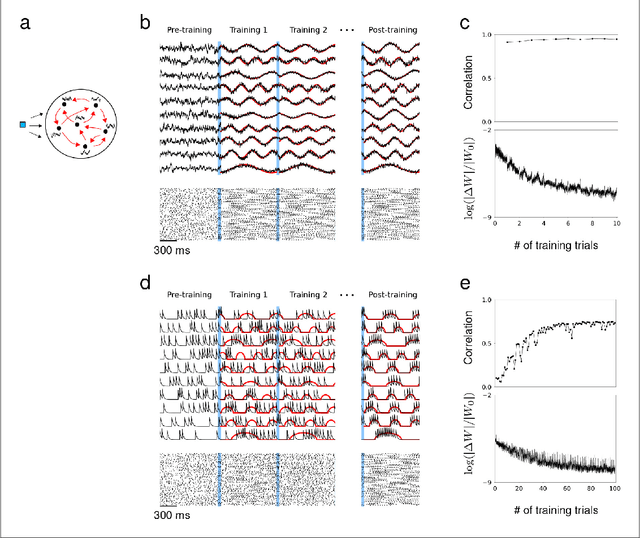
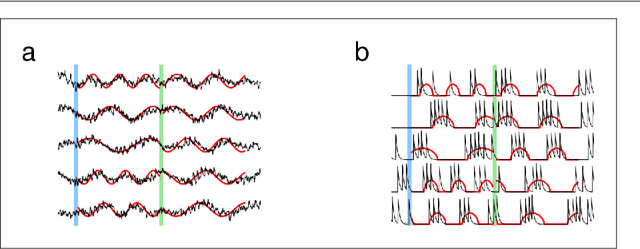
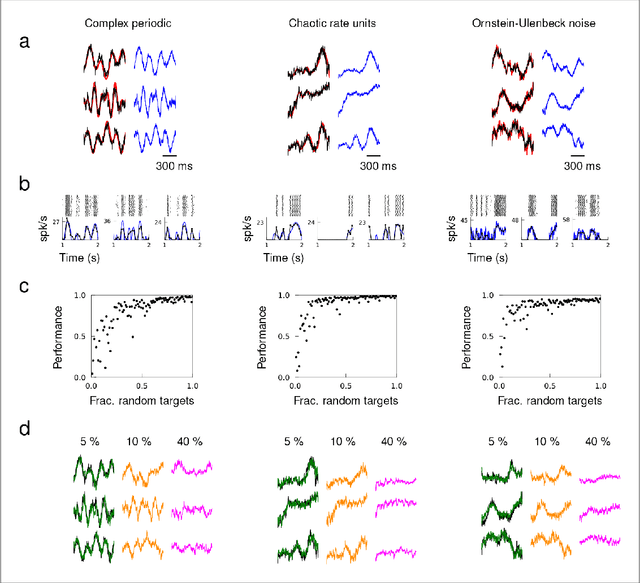
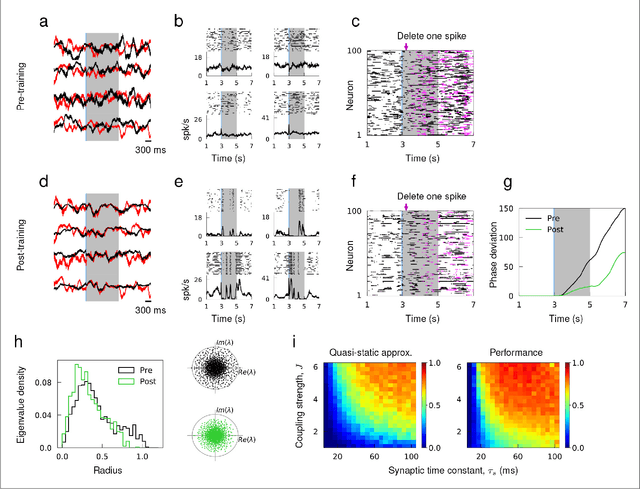
Spiking activity of neurons engaged in learning and performing a task show complex spatiotemporal dynamics. While the output of recurrent network models can learn to perform various tasks, the possible range of recurrent dynamics that emerge after learning remains unknown. Here we show that modifying the recurrent connectivity with a recursive least squares algorithm provides sufficient flexibility for synaptic and spiking rate dynamics of spiking networks to produce a wide range of spatiotemporal activity. We apply the training method to learn arbitrary firing patterns, stabilize irregular spiking activity of a balanced network, and reproduce the heterogeneous spiking rate patterns of cortical neurons engaged in motor planning and movement. We identify sufficient conditions for successful learning, characterize two types of learning errors, and assess the network capacity. Our findings show that synaptically-coupled recurrent spiking networks possess a vast computational capability that can support the diverse activity patterns in the brain.