Stepsize Learning for Policy Gradient Methods in Contextual Markov Decision Processes

Policy-based algorithms are among the most widely adopted techniques in model-free RL, thanks to their strong theoretical groundings and good properties in continuous action spaces. Unfortunately, these methods require precise and problem-specific hyperparameter tuning to achieve good performance, and tend to struggle when asked to accomplish a series of heterogeneous tasks. In particular, the selection of the step size has a crucial impact on their ability to learn a highly performing policy, affecting the speed and the stability of the training process, and often being the main culprit for poor results. In this paper, we tackle these issues with a Meta Reinforcement Learning approach, by introducing a new formulation, known as meta-MDP, that can be used to solve any hyperparameter selection problem in RL with contextual processes. After providing a theoretical Lipschitz bound to the difference of performance in different tasks, we adopt the proposed framework to train a batch RL algorithm to dynamically recommend the most adequate step size for different policies and tasks. In conclusion, we present an experimental campaign to show the advantages of selecting an adaptive learning rate in heterogeneous environments.

Simultaneously Updating All Persistence Values in Reinforcement Learning

In reinforcement learning, the performance of learning agents is highly sensitive to the choice of time discretization. Agents acting at high frequencies have the best control opportunities, along with some drawbacks, such as possible inefficient exploration and vanishing of the action advantages. The repetition of the actions, i.e., action persistence, comes into help, as it allows the agent to visit wider regions of the state space and improve the estimation of the action effects. In this work, we derive a novel All-Persistence Bellman Operator, which allows an effective use of both the low-persistence experience, by decomposition into sub-transition, and the high-persistence experience, thanks to the introduction of a suitable bootstrap procedure. In this way, we employ transitions collected at any time scale to update simultaneously the action values of the considered persistence set. We prove the contraction property of the All-Persistence Bellman Operator and, based on it, we extend classic Q-learning and DQN. After providing a study on the effects of persistence, we experimentally evaluate our approach in both tabular contexts and more challenging frameworks, including some Atari games.

Control Frequency Adaptation via Action Persistence in Batch Reinforcement Learning

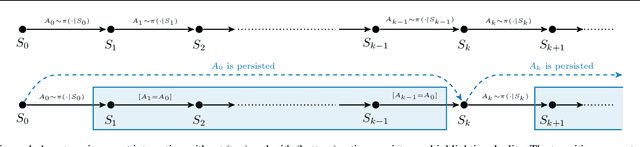
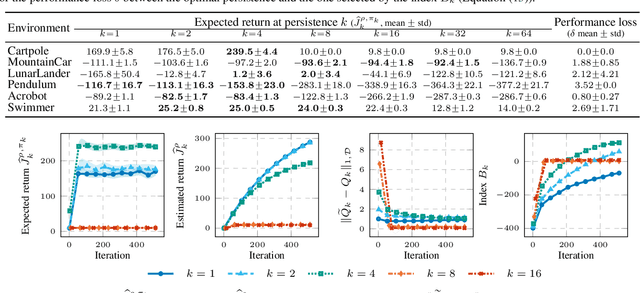
The choice of the control frequency of a system has a relevant impact on the ability of reinforcement learning algorithms to learn a highly performing policy. In this paper, we introduce the notion of action persistence that consists in the repetition of an action for a fixed number of decision steps, having the effect of modifying the control frequency. We start analyzing how action persistence affects the performance of the optimal policy, and then we present a novel algorithm, Persistent Fitted Q-Iteration (PFQI), that extends FQI, with the goal of learning the optimal value function at a given persistence. After having provided a theoretical study of PFQI and a heuristic approach to identify the optimal persistence, we present an experimental campaign on benchmark domains to show the advantages of action persistence and proving the effectiveness of our persistence selection method.

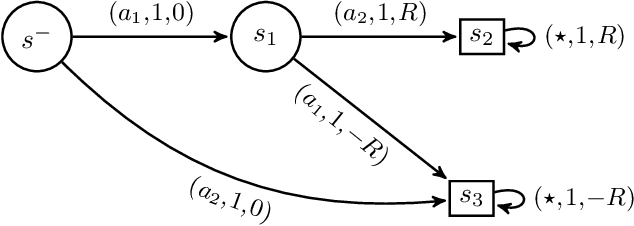
Risk-Averse Trust Region Optimization for Reward-Volatility Reduction

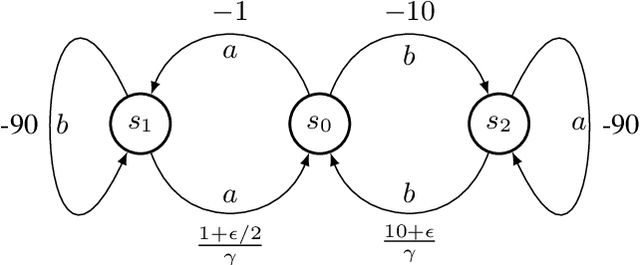
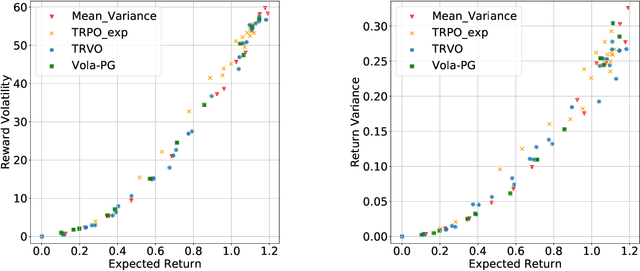
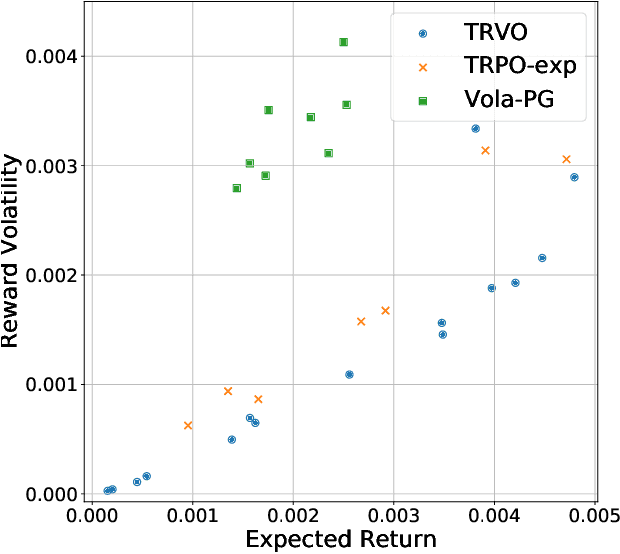
In real-world decision-making problems, for instance in the fields of finance, robotics or autonomous driving, keeping uncertainty under control is as important as maximizing expected returns. Risk aversion has been addressed in the reinforcement learning literature through risk measures related to the variance of returns. However, in many cases, the risk is measured not only on a long-term perspective, but also on the step-wise rewards (e.g., in trading, to ensure the stability of the investment bank, it is essential to monitor the risk of portfolio positions on a daily basis). In this paper, we define a novel measure of risk, which we call reward volatility, consisting of the variance of the rewards under the state-occupancy measure. We show that the reward volatility bounds the return variance so that reducing the former also constrains the latter. We derive a policy gradient theorem with a new objective function that exploits the mean-volatility relationship, and develop an actor-only algorithm. Furthermore, thanks to the linearity of the Bellman equations defined under the new objective function, it is possible to adapt the well-known policy gradient algorithms with monotonic improvement guarantees such as TRPO in a risk-averse manner. Finally, we test the proposed approach in two simulated financial environments.