Risk-Averse Trust Region Optimization for Reward-Volatility Reduction
Paper and Code
Dec 06, 2019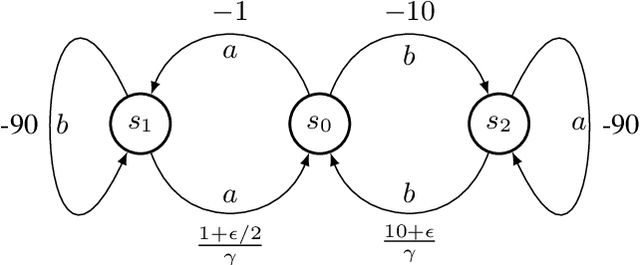
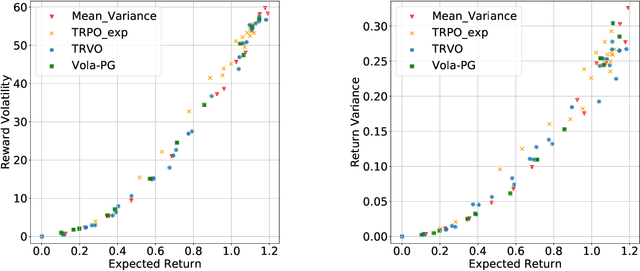
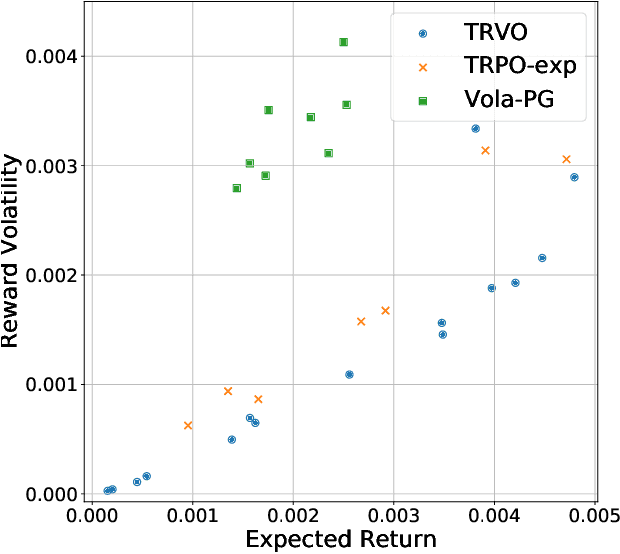
In real-world decision-making problems, for instance in the fields of finance, robotics or autonomous driving, keeping uncertainty under control is as important as maximizing expected returns. Risk aversion has been addressed in the reinforcement learning literature through risk measures related to the variance of returns. However, in many cases, the risk is measured not only on a long-term perspective, but also on the step-wise rewards (e.g., in trading, to ensure the stability of the investment bank, it is essential to monitor the risk of portfolio positions on a daily basis). In this paper, we define a novel measure of risk, which we call reward volatility, consisting of the variance of the rewards under the state-occupancy measure. We show that the reward volatility bounds the return variance so that reducing the former also constrains the latter. We derive a policy gradient theorem with a new objective function that exploits the mean-volatility relationship, and develop an actor-only algorithm. Furthermore, thanks to the linearity of the Bellman equations defined under the new objective function, it is possible to adapt the well-known policy gradient algorithms with monotonic improvement guarantees such as TRPO in a risk-averse manner. Finally, we test the proposed approach in two simulated financial environments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge