Optimal Execution with Reinforcement Learning

This study investigates the development of an optimal execution strategy through reinforcement learning, aiming to determine the most effective approach for traders to buy and sell inventory within a limited time frame. Our proposed model leverages input features derived from the current state of the limit order book. To simulate this environment and overcome the limitations associated with relying on historical data, we utilize the multi-agent market simulator ABIDES, which provides a diverse range of depth levels within the limit order book. We present a custom MDP formulation followed by the results of our methodology and benchmark the performance against standard execution strategies. Our findings suggest that the reinforcement learning-based approach demonstrates significant potential.

Reinforcement Learning for Credit Index Option Hedging

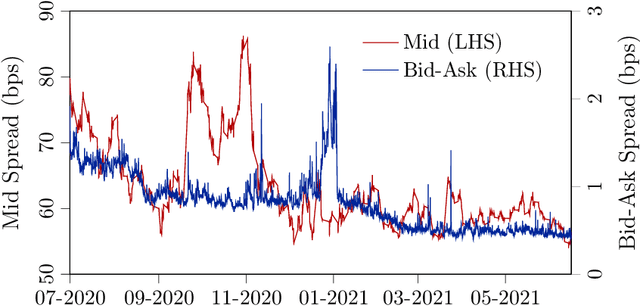
In this paper, we focus on finding the optimal hedging strategy of a credit index option using reinforcement learning. We take a practical approach, where the focus is on realism i.e. discrete time, transaction costs; even testing our policy on real market data. We apply a state of the art algorithm, the Trust Region Volatility Optimization (TRVO) algorithm and show that the derived hedging strategy outperforms the practitioner's Black & Scholes delta hedge.

Option Hedging with Risk Averse Reinforcement Learning

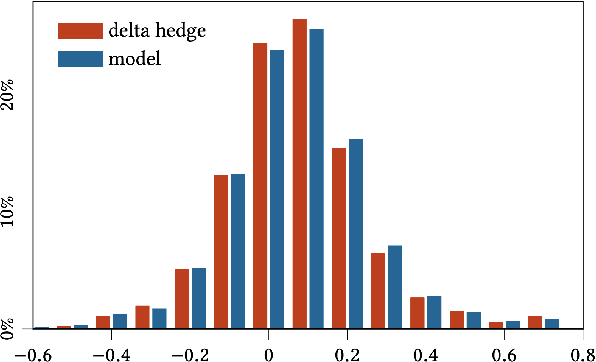
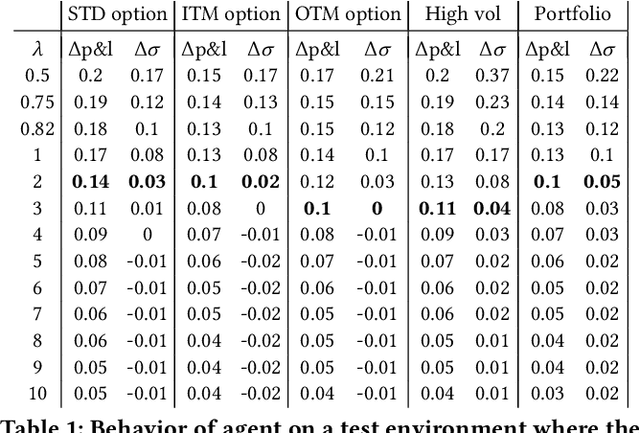
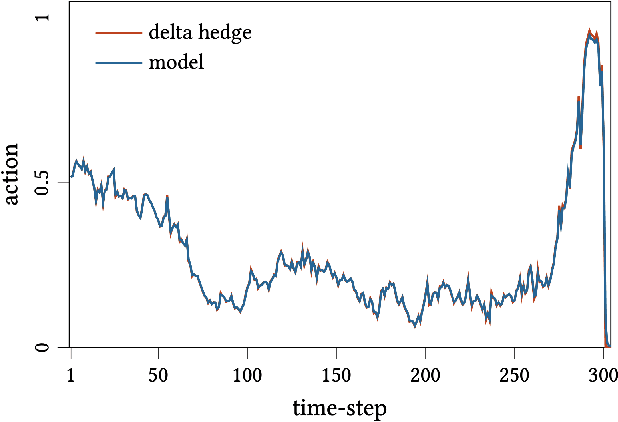
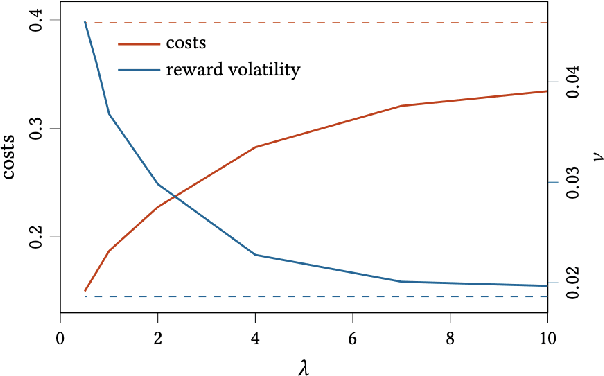
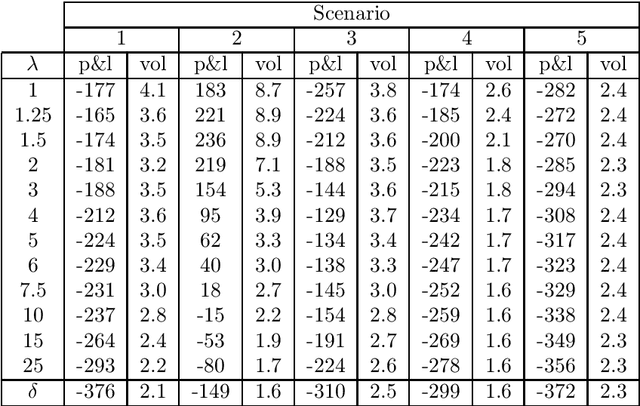
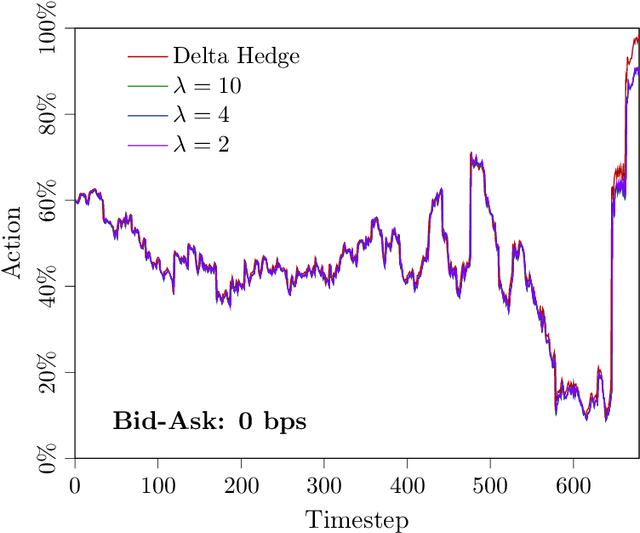
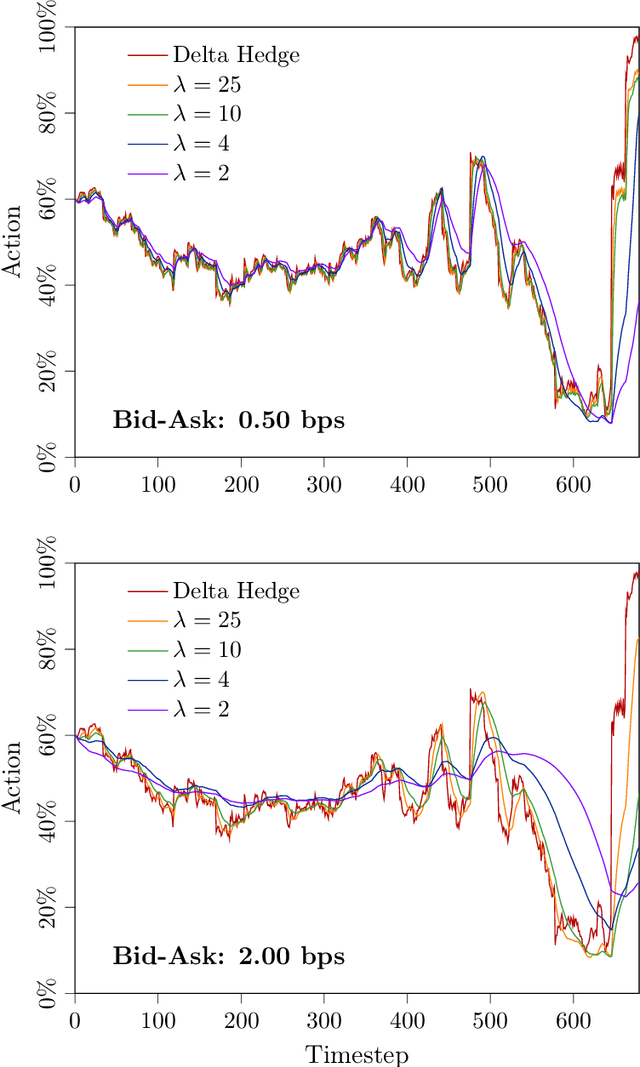
In this paper we show how risk-averse reinforcement learning can be used to hedge options. We apply a state-of-the-art risk-averse algorithm: Trust Region Volatility Optimization (TRVO) to a vanilla option hedging environment, considering realistic factors such as discrete time and transaction costs. Realism makes the problem twofold: the agent must both minimize volatility and contain transaction costs, these tasks usually being in competition. We use the algorithm to train a sheaf of agents each characterized by a different risk aversion, so to be able to span an efficient frontier on the volatility-p\&l space. The results show that the derived hedging strategy not only outperforms the Black \& Scholes delta hedge, but is also extremely robust and flexible, as it can efficiently hedge options with different characteristics and work on markets with different behaviors than what was used in training.

Risk-Averse Trust Region Optimization for Reward-Volatility Reduction

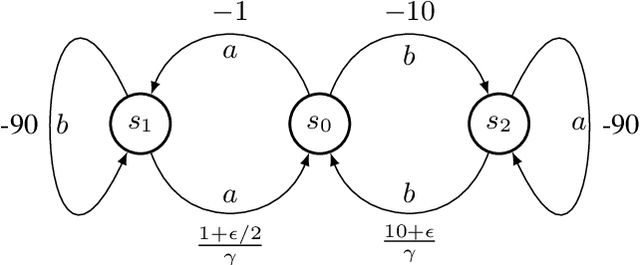
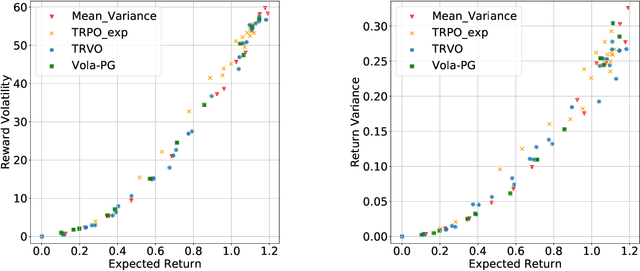
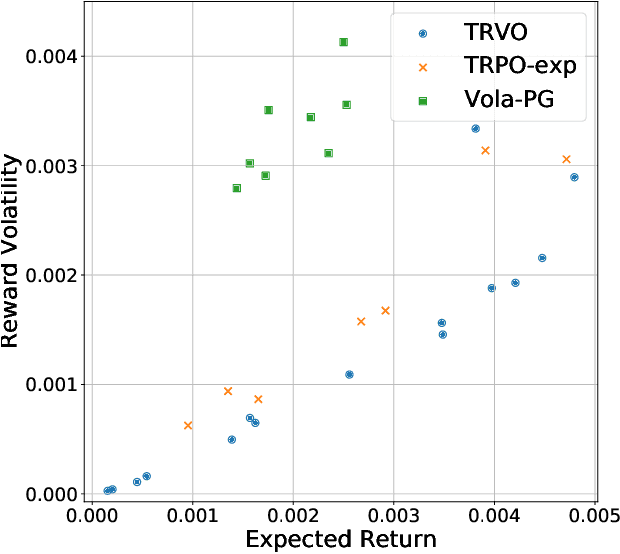
In real-world decision-making problems, for instance in the fields of finance, robotics or autonomous driving, keeping uncertainty under control is as important as maximizing expected returns. Risk aversion has been addressed in the reinforcement learning literature through risk measures related to the variance of returns. However, in many cases, the risk is measured not only on a long-term perspective, but also on the step-wise rewards (e.g., in trading, to ensure the stability of the investment bank, it is essential to monitor the risk of portfolio positions on a daily basis). In this paper, we define a novel measure of risk, which we call reward volatility, consisting of the variance of the rewards under the state-occupancy measure. We show that the reward volatility bounds the return variance so that reducing the former also constrains the latter. We derive a policy gradient theorem with a new objective function that exploits the mean-volatility relationship, and develop an actor-only algorithm. Furthermore, thanks to the linearity of the Bellman equations defined under the new objective function, it is possible to adapt the well-known policy gradient algorithms with monotonic improvement guarantees such as TRPO in a risk-averse manner. Finally, we test the proposed approach in two simulated financial environments.