Compressive Clustering with an Optical Processing Unit

We explore the use of Optical Processing Units (OPU) to compute random Fourier features for sketching, and adapt the overall compressive clustering pipeline to this setting. We also propose some tools to help tuning a critical hyper-parameter of compressive clustering.

Deep Networks with Adaptive Nyström Approximation

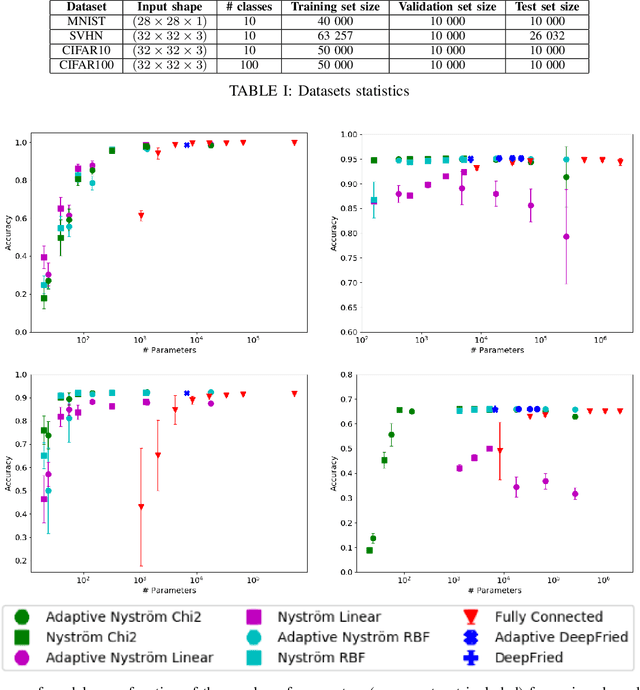
Recent work has focused on combining kernel methods and deep learning to exploit the best of the two approaches. Here, we introduce a new architecture of neural networks in which we replace the top dense layers of standard convolutional architectures with an approximation of a kernel function by relying on the Nystr{\"o}m approximation. Our approach is easy and highly flexible. It is compatible with any kernel function and it allows exploiting multiple kernels. We show that our architecture has the same performance than standard architecture on datasets like SVHN and CIFAR100. One benefit of the method lies in its limited number of learnable parameters which makes it particularly suited for small training set sizes, e.g. from 5 to 20 samples per class.

QuicK-means: Acceleration of K-means by learning a fast transform

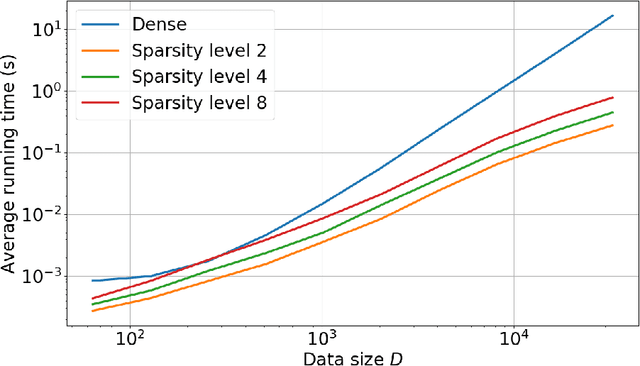
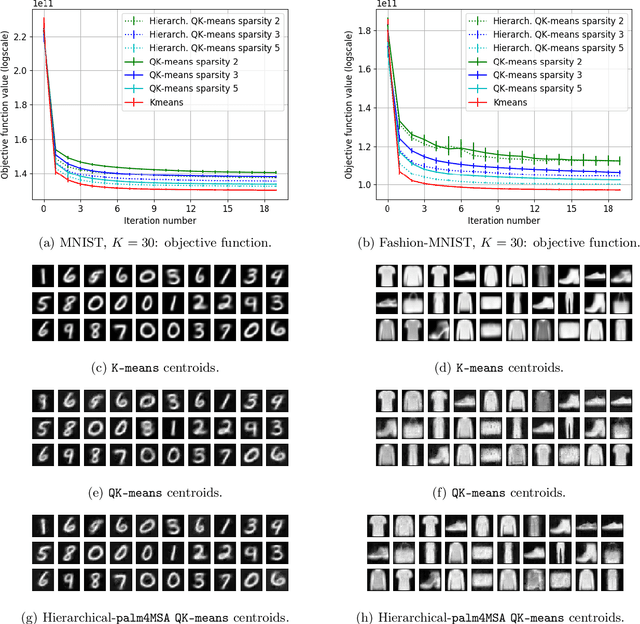
K-means -- and the celebrated Lloyd algorithm -- is more than the clustering method it was originally designed to be. It has indeed proven pivotal to help increase the speed of many machine learning and data analysis techniques such as indexing, nearest-neighbor search and prediction, data compression; its beneficial use has been shown to carry over to the acceleration of kernel machines (when using the Nystr\"om method). Here, we propose a fast extension of K-means, dubbed QuicK-means, that rests on the idea of expressing the matrix of the $K$ centroids as a product of sparse matrices, a feat made possible by recent results devoted to find approximations of matrices as a product of sparse factors. Using such a decomposition squashes the complexity of the matrix-vector product between the factorized $K \times D$ centroid matrix $\mathbf{U}$ and any vector from $\mathcal{O}(K D)$ to $\mathcal{O}(A \log A+B)$, with $A=\min (K, D)$ and $B=\max (K, D)$, where $D$ is the dimension of the training data. This drastic computational saving has a direct impact in the assignment process of a point to a cluster, meaning that it is not only tangible at prediction time, but also at training time, provided the factorization procedure is performed during Lloyd's algorithm. We precisely show that resorting to a factorization step at each iteration does not impair the convergence of the optimization scheme and that, depending on the context, it may entail a reduction of the training time. Finally, we provide discussions and numerical simulations that show the versatility of our computationally-efficient QuicK-means algorithm.