Self-Supervised Learning to Prove Equivalence Between Programs via Semantics-Preserving Rewrite Rules

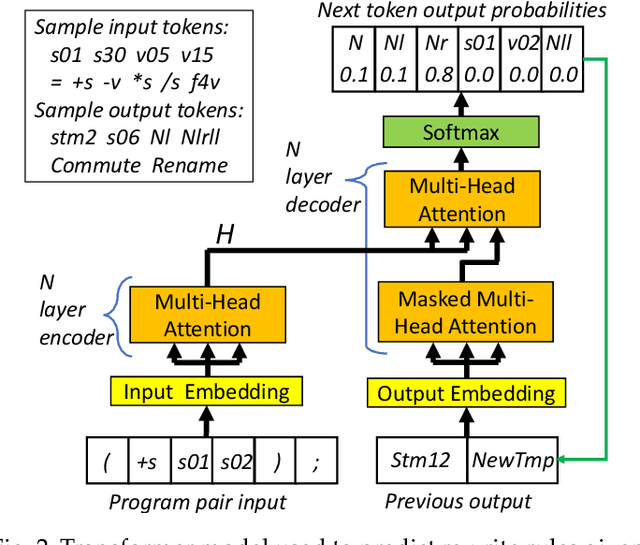
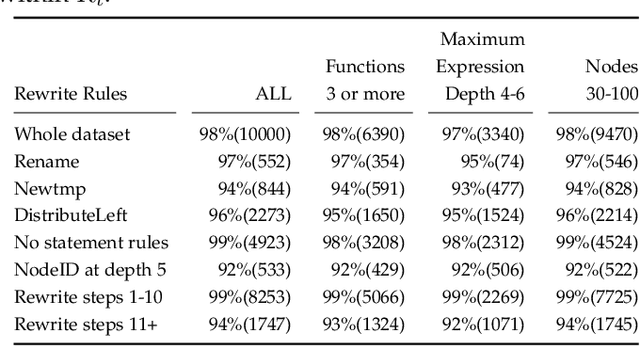
We target the problem of synthesizing proofs of semantic equivalence between two programs made of sequences of statements with complex symbolic expressions. We propose a neural network architecture based on the transformer to generate axiomatic proofs of equivalence between program pairs. We generate expressions which include scalars and vectors and support multi-typed rewrite rules to prove equivalence. For training the system, we develop an original training technique, which we call self-supervised sample selection. This incremental training improves the quality, generalizability and extensibility of the learned model. We study the effectiveness of the system to generate proofs of increasing length, and we demonstrate how transformer models learn to represent complex and verifiable symbolic reasoning. Our system, S4Eq, achieves 97% proof success on 10,000 pairs of programs while ensuring zero false positives by design.

Proving Equivalence Between Complex Expressions Using Graph-to-Sequence Neural Models

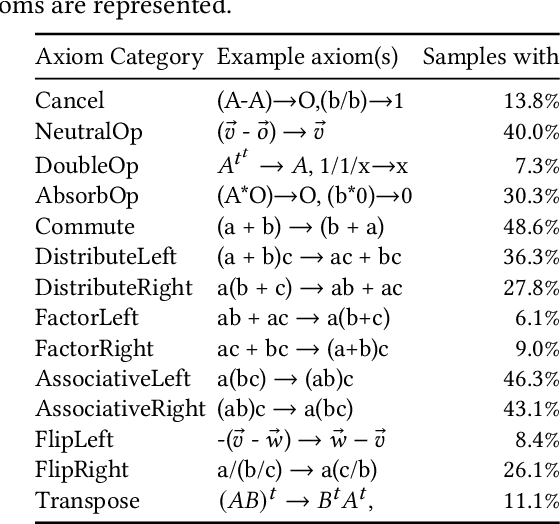
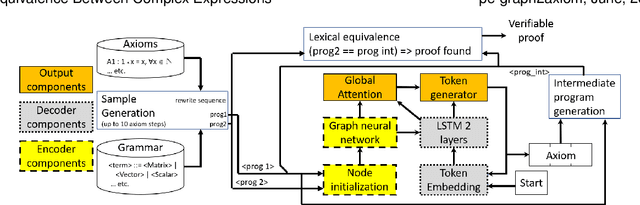
We target the problem of provably computing the equivalence between two complex expression trees. To this end, we formalize the problem of equivalence between two such programs as finding a set of semantics-preserving rewrite rules from one into the other, such that after the rewrite the two programs are structurally identical, and therefore trivially equivalent.We then develop a graph-to-sequence neural network system for program equivalence, trained to produce such rewrite sequences from a carefully crafted automatic example generation algorithm. We extensively evaluate our system on a rich multi-type linear algebra expression language, using arbitrary combinations of 100+ graph-rewriting axioms of equivalence. Our machine learning system guarantees correctness for all true negatives, and ensures 0 false positive by design. It outputs via inference a valid proof of equivalence for 93% of the 10,000 equivalent expression pairs isolated for testing, using up to 50-term expressions. In all cases, the validity of the sequence produced and therefore the provable assertion of program equivalence is always computable, in negligible time.

Equivalence of Dataflow Graphs via Rewrite Rules Using a Graph-to-Sequence Neural Model

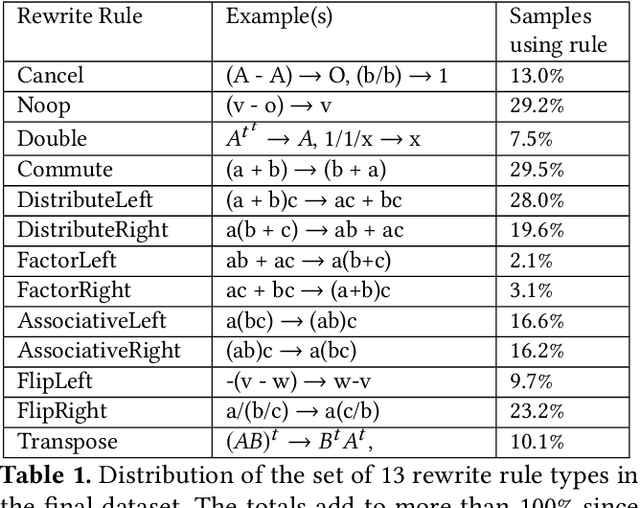
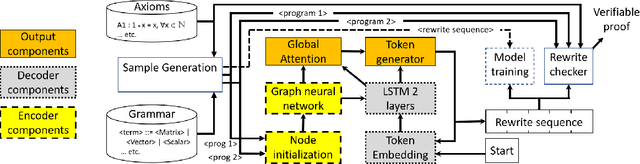
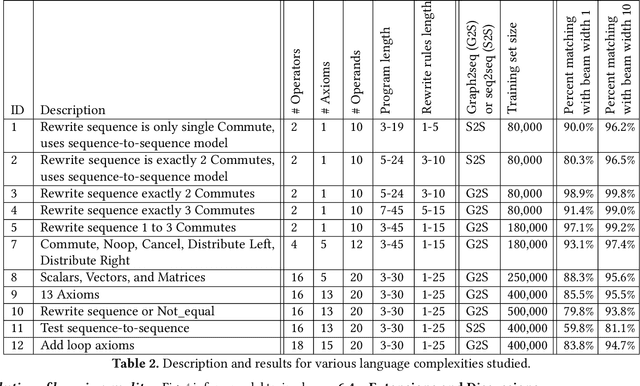
In this work we target the problem of provably computing the equivalence between two programs represented as dataflow graphs. To this end, we formalize the problem of equivalence between two programs as finding a set of semantics-preserving rewrite rules from one into the other, such that after the rewrite the two programs are structurally identical, and therefore trivially equivalent. We then develop the first graph-to-sequence neural network system for program equivalence, trained to produce such rewrite sequences from a carefully crafted automatic example generation algorithm. We extensively evaluate our system on a rich multi-type linear algebra expression language, using arbitrary combinations of 100+ graph-rewriting axioms of equivalence. Our system outputs via inference a correct rewrite sequence for 96% of the 10,000 program pairs isolated for testing, using 30-term programs. And in all cases, the validity of the sequence produced and therefore the provable assertion of program equivalence is computable, in negligible time.

SequenceR: Sequence-to-Sequence Learning for End-to-End Program Repair

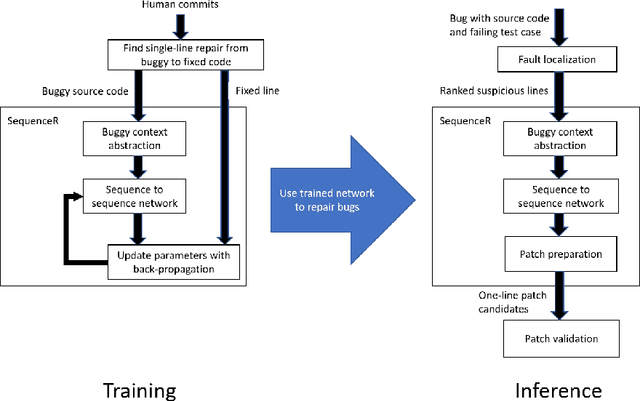
This paper presents a novel end-to-end approach to program repair based on sequence-to-sequence learning. We devise, implement, and evaluate a system, called SequenceR, for fixing bugs based on sequence-to-sequence learning on source code. This approach uses the copy mechanism to overcome the unlimited vocabulary problem that occurs with big code. Our system is data-driven; we train it on 35,578 commits, carefully curated from open-source repositories. We evaluate it on 4,711 independent real bug fixes, as well on the Defects4J benchmark used in program repair research. SequenceR is able to perfectly predict the fixed line for 950/4711 testing samples. It captures a wide range of repair operators without any domain-specific top-down design.