Self-Supervised Learning to Prove Equivalence Between Programs via Semantics-Preserving Rewrite Rules
Paper and Code
Sep 22, 2021

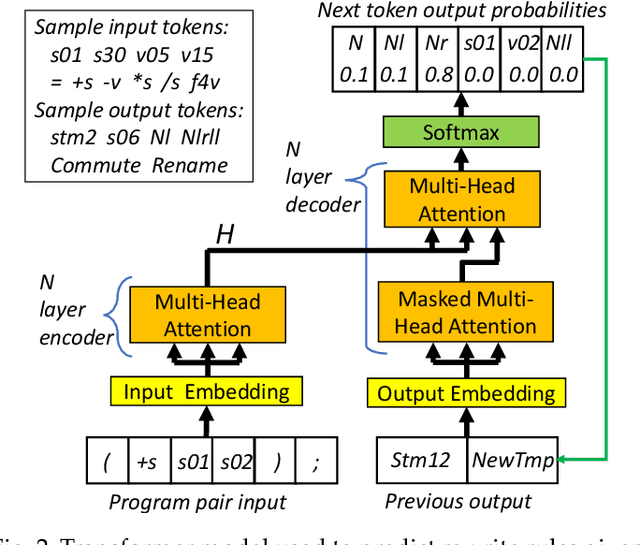
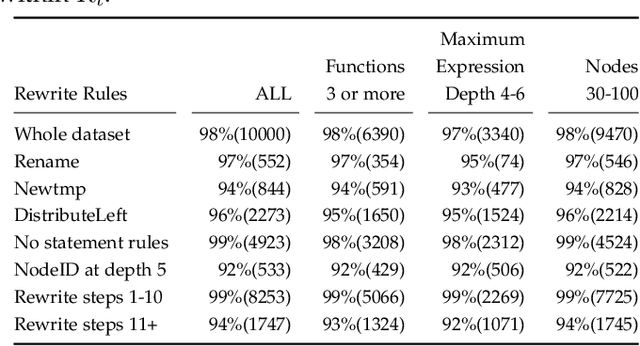
We target the problem of synthesizing proofs of semantic equivalence between two programs made of sequences of statements with complex symbolic expressions. We propose a neural network architecture based on the transformer to generate axiomatic proofs of equivalence between program pairs. We generate expressions which include scalars and vectors and support multi-typed rewrite rules to prove equivalence. For training the system, we develop an original training technique, which we call self-supervised sample selection. This incremental training improves the quality, generalizability and extensibility of the learned model. We study the effectiveness of the system to generate proofs of increasing length, and we demonstrate how transformer models learn to represent complex and verifiable symbolic reasoning. Our system, S4Eq, achieves 97% proof success on 10,000 pairs of programs while ensuring zero false positives by design.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge