Proving Equivalence Between Complex Expressions Using Graph-to-Sequence Neural Models

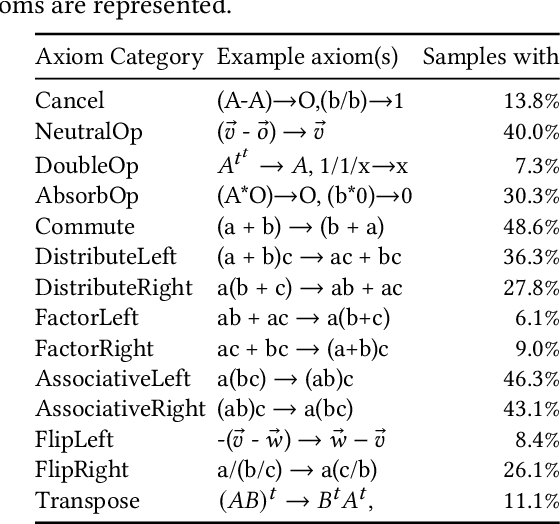
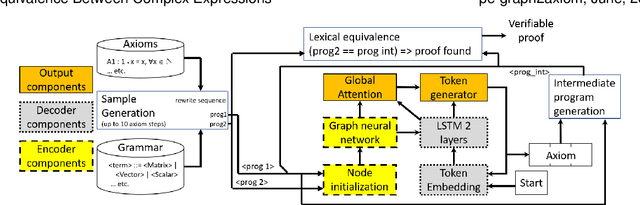
We target the problem of provably computing the equivalence between two complex expression trees. To this end, we formalize the problem of equivalence between two such programs as finding a set of semantics-preserving rewrite rules from one into the other, such that after the rewrite the two programs are structurally identical, and therefore trivially equivalent.We then develop a graph-to-sequence neural network system for program equivalence, trained to produce such rewrite sequences from a carefully crafted automatic example generation algorithm. We extensively evaluate our system on a rich multi-type linear algebra expression language, using arbitrary combinations of 100+ graph-rewriting axioms of equivalence. Our machine learning system guarantees correctness for all true negatives, and ensures 0 false positive by design. It outputs via inference a valid proof of equivalence for 93% of the 10,000 equivalent expression pairs isolated for testing, using up to 50-term expressions. In all cases, the validity of the sequence produced and therefore the provable assertion of program equivalence is always computable, in negligible time.

Equivalence of Dataflow Graphs via Rewrite Rules Using a Graph-to-Sequence Neural Model

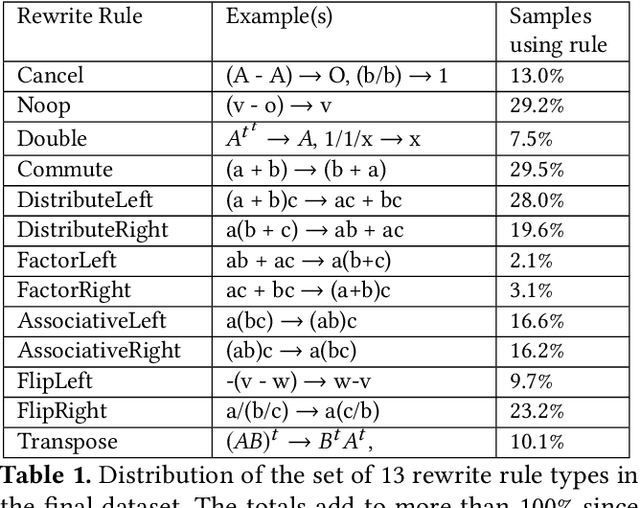
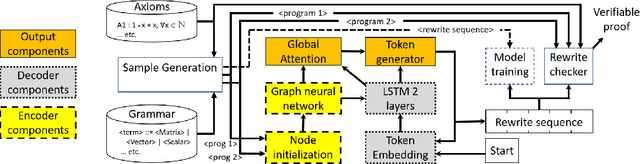
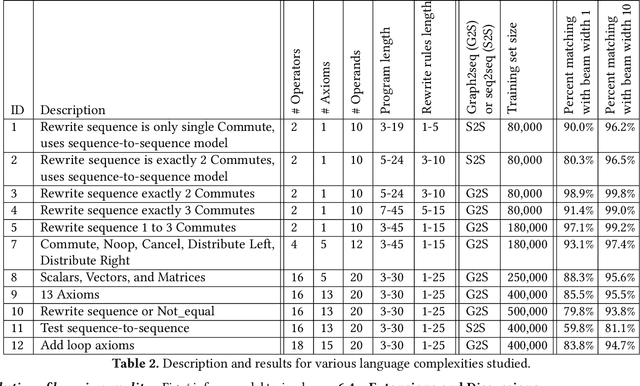
In this work we target the problem of provably computing the equivalence between two programs represented as dataflow graphs. To this end, we formalize the problem of equivalence between two programs as finding a set of semantics-preserving rewrite rules from one into the other, such that after the rewrite the two programs are structurally identical, and therefore trivially equivalent. We then develop the first graph-to-sequence neural network system for program equivalence, trained to produce such rewrite sequences from a carefully crafted automatic example generation algorithm. We extensively evaluate our system on a rich multi-type linear algebra expression language, using arbitrary combinations of 100+ graph-rewriting axioms of equivalence. Our system outputs via inference a correct rewrite sequence for 96% of the 10,000 program pairs isolated for testing, using 30-term programs. And in all cases, the validity of the sequence produced and therefore the provable assertion of program equivalence is computable, in negligible time.