Louis Fortier-Dubois
Learning Aggregations of Binary Activated Neural Networks with Probabilities over Representations
Oct 29, 2021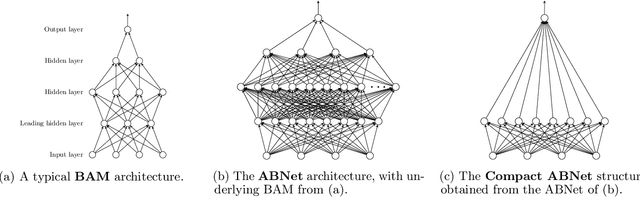
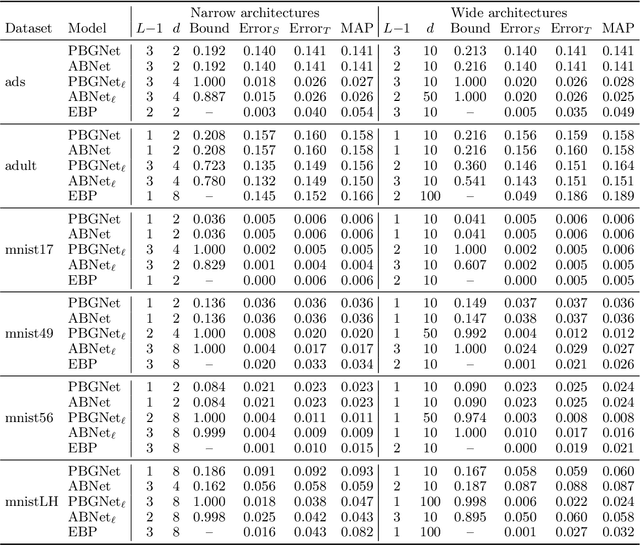
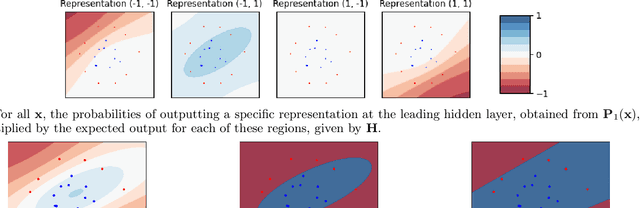
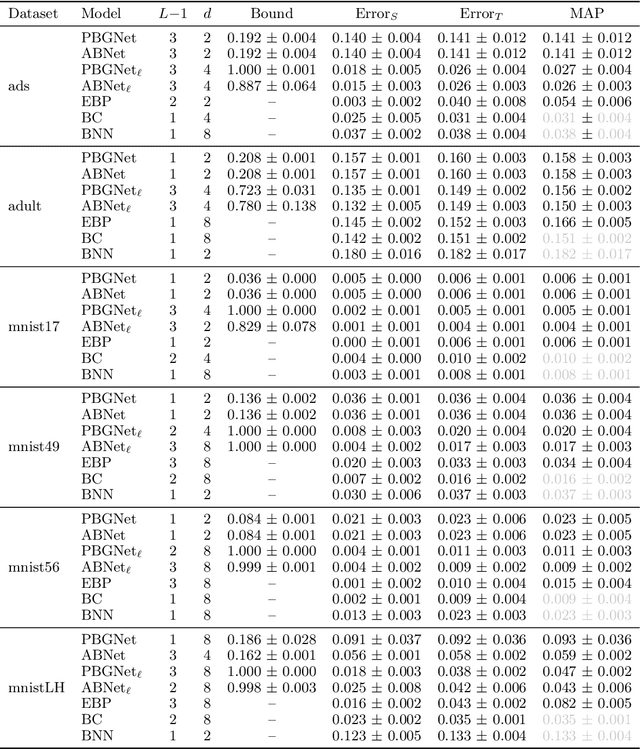
Abstract:Considering a probability distribution over parameters is known as an efficient strategy to learn a neural network with non-differentiable activation functions. We study the expectation of a probabilistic neural network as a predictor by itself, focusing on the aggregation of binary activated neural networks with normal distributions over real-valued weights. Our work leverages a recent analysis derived from the PAC-Bayesian framework that derives tight generalization bounds and learning procedures for the expected output value of such an aggregation, which is given by an analytical expression. While the combinatorial nature of the latter has been circumvented by approximations in previous works, we show that the exact computation remains tractable for deep but narrow neural networks, thanks to a dynamic programming approach. This leads us to a peculiar bound minimization learning algorithm for binary activated neural networks, where the forward pass propagates probabilities over representations instead of activation values. A stochastic counterpart of this new neural networks training scheme that scales to wider architectures is proposed.
Efficient Learning of Ensembles with QuadBoost
Nov 20, 2015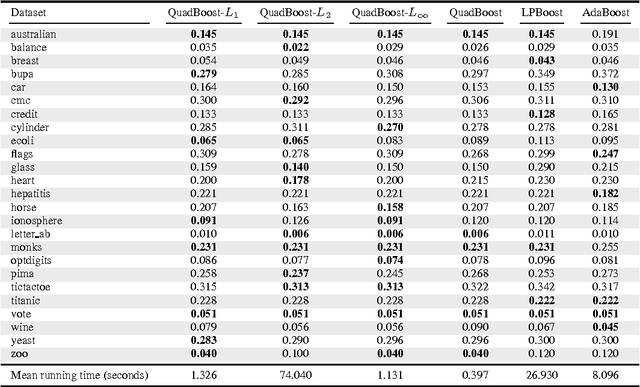
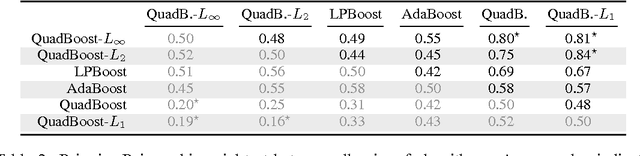
Abstract:We first present a general risk bound for ensembles that depends on the Lp norm of the weighted combination of voters which can be selected from a continuous set. We then propose a boosting method, called QuadBoost, which is strongly supported by the general risk bound and has very simple rules for assigning the voters' weights. Moreover, QuadBoost exhibits a rate of decrease of its empirical error which is slightly faster than the one achieved by AdaBoost. The experimental results confirm the expectation of the theory that QuadBoost is a very efficient method for learning ensembles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge