Sample Compression Hypernetworks: From Generalization Bounds to Meta-Learning

Reconstruction functions are pivotal in sample compression theory, a framework for deriving tight generalization bounds. From a small sample of the training set (the compression set) and an optional stream of information (the message), they recover a predictor previously learned from the whole training set. While usually fixed, we propose to learn reconstruction functions. To facilitate the optimization and increase the expressiveness of the message, we derive a new sample compression generalization bound for real-valued messages. From this theoretical analysis, we then present a new hypernetwork architecture that outputs predictors with tight generalization guarantees when trained using an original meta-learning framework. The results of promising preliminary experiments are then reported.

Interpretability in Machine Learning: on the Interplay with Explainability, Predictive Performances and Models

Interpretability has recently gained attention in the field of machine learning, for it is crucial when it comes to high-stakes decisions or troubleshooting. This abstract concept is hard to grasp and has been associated, over time, with many labels and preconceived ideas. In this position paper, in order to clarify some misunderstandings regarding interpretability, we discuss its relationship with significant concepts in machine learning: explainability, predictive performances, and machine learning models. For instance, we challenge the idea that interpretability and explainability are substitutes to one another, or that a fixed degree of interpretability can be associated with a given machine learning model.

A Greedy Algorithm for Building Compact Binary Activated Neural Networks

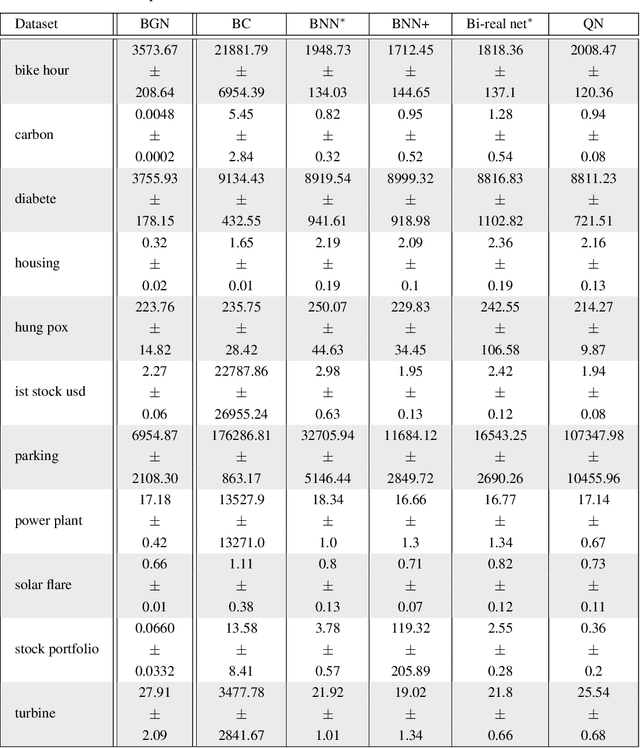
We study binary activated neural networks in the context of regression tasks, provide guarantees on the expressiveness of these particular networks and propose a greedy algorithm for building such networks. Aiming for predictors having small resources needs, the greedy approach does not need to fix in advance an architecture for the network: this one is built one layer at a time, one neuron at a time, leading to predictors that aren't needlessly wide and deep for a given task. Similarly to boosting algorithms, our approach guarantees a training loss reduction every time a neuron is added to a layer. This greatly differs from most binary activated neural networks training schemes that rely on stochastic gradient descent (circumventing the 0-almost-everywhere derivative problem of the binary activation function by surrogates such as the straight through estimator or continuous binarization). We show that our method provides compact and sparse predictors while obtaining similar performances to state-of-the-art methods for training binary activated networks.

Learning Aggregations of Binary Activated Neural Networks with Probabilities over Representations

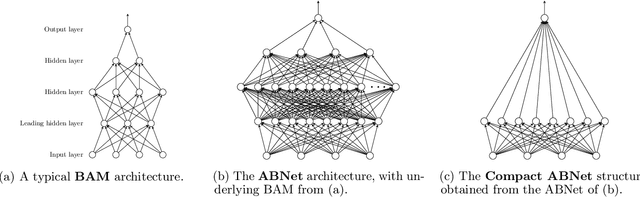
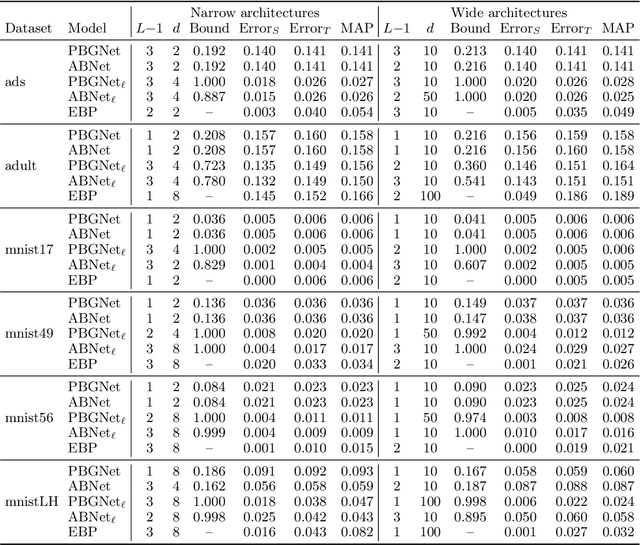
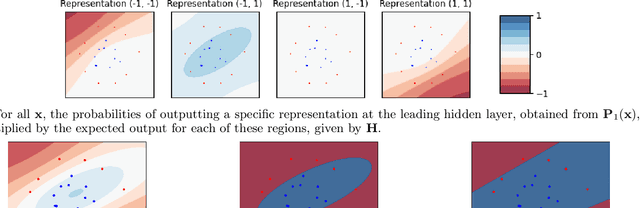
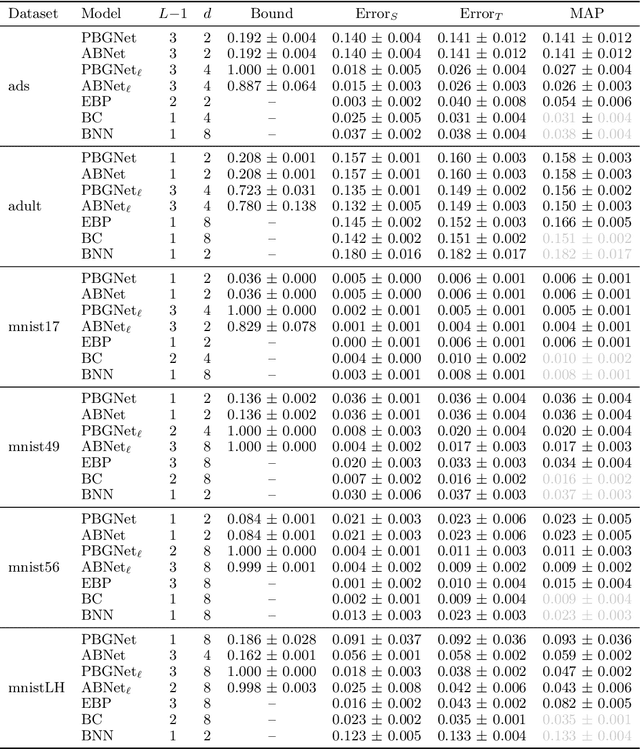
Considering a probability distribution over parameters is known as an efficient strategy to learn a neural network with non-differentiable activation functions. We study the expectation of a probabilistic neural network as a predictor by itself, focusing on the aggregation of binary activated neural networks with normal distributions over real-valued weights. Our work leverages a recent analysis derived from the PAC-Bayesian framework that derives tight generalization bounds and learning procedures for the expected output value of such an aggregation, which is given by an analytical expression. While the combinatorial nature of the latter has been circumvented by approximations in previous works, we show that the exact computation remains tractable for deep but narrow neural networks, thanks to a dynamic programming approach. This leads us to a peculiar bound minimization learning algorithm for binary activated neural networks, where the forward pass propagates probabilities over representations instead of activation values. A stochastic counterpart of this new neural networks training scheme that scales to wider architectures is proposed.