Sample Compression for Continual Learning

Continual learning algorithms aim to learn from a sequence of tasks, making the training distribution non-stationary. The majority of existing continual learning approaches in the literature rely on heuristics and do not provide learning guarantees for the continual learning setup. In this paper, we present a new method called 'Continual Pick-to-Learn' (CoP2L), which is able to retain the most representative samples for each task in an efficient way. The algorithm is adapted from the Pick-to-Learn algorithm, rooted in the sample compression theory. This allows us to provide high-confidence upper bounds on the generalization loss of the learned predictors, numerically computable after every update of the learned model. We also empirically show on several standard continual learning benchmarks that our algorithm is able to outperform standard experience replay, significantly mitigating catastrophic forgetting.

Sample Compression Hypernetworks: From Generalization Bounds to Meta-Learning

Reconstruction functions are pivotal in sample compression theory, a framework for deriving tight generalization bounds. From a small sample of the training set (the compression set) and an optional stream of information (the message), they recover a predictor previously learned from the whole training set. While usually fixed, we propose to learn reconstruction functions. To facilitate the optimization and increase the expressiveness of the message, we derive a new sample compression generalization bound for real-valued messages. From this theoretical analysis, we then present a new hypernetwork architecture that outputs predictors with tight generalization guarantees when trained using an original meta-learning framework. The results of promising preliminary experiments are then reported.

Sample compression unleashed : New generalization bounds for real valued losses

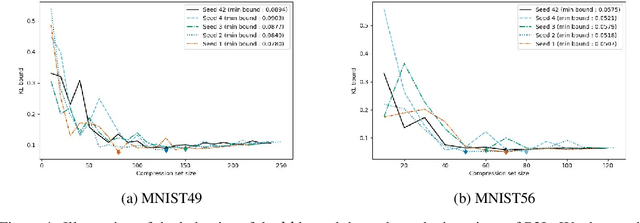
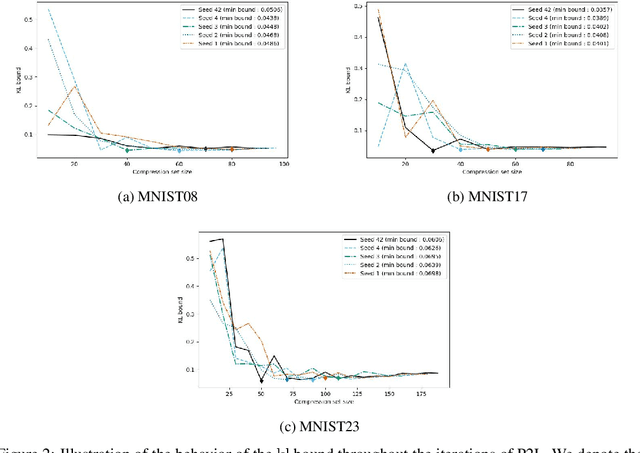
The sample compression theory provides generalization guarantees for predictors that can be fully defined using a subset of the training dataset and a (short) message string, generally defined as a binary sequence. Previous works provided generalization bounds for the zero-one loss, which is restrictive, notably when applied to deep learning approaches. In this paper, we present a general framework for deriving new sample compression bounds that hold for real-valued losses. We empirically demonstrate the tightness of the bounds and their versatility by evaluating them on different types of models, e.g., neural networks and decision forests, trained with the Pick-To-Learn (P2L) meta-algorithm, which transforms the training method of any machine-learning predictor to yield sample-compressed predictors. In contrast to existing P2L bounds, ours are valid in the non-consistent case.