A Greedy Algorithm for Building Compact Binary Activated Neural Networks

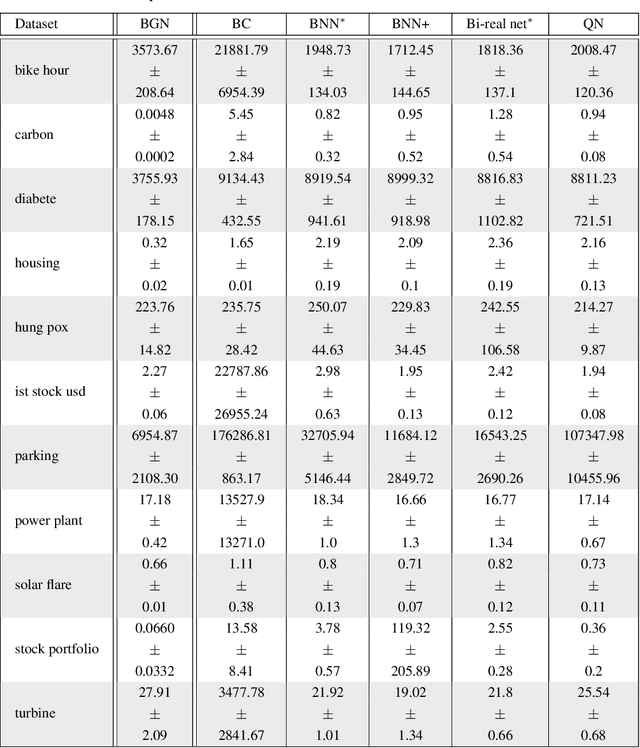
We study binary activated neural networks in the context of regression tasks, provide guarantees on the expressiveness of these particular networks and propose a greedy algorithm for building such networks. Aiming for predictors having small resources needs, the greedy approach does not need to fix in advance an architecture for the network: this one is built one layer at a time, one neuron at a time, leading to predictors that aren't needlessly wide and deep for a given task. Similarly to boosting algorithms, our approach guarantees a training loss reduction every time a neuron is added to a layer. This greatly differs from most binary activated neural networks training schemes that rely on stochastic gradient descent (circumventing the 0-almost-everywhere derivative problem of the binary activation function by surrogates such as the straight through estimator or continuous binarization). We show that our method provides compact and sparse predictors while obtaining similar performances to state-of-the-art methods for training binary activated networks.