Learning Aggregations of Binary Activated Neural Networks with Probabilities over Representations

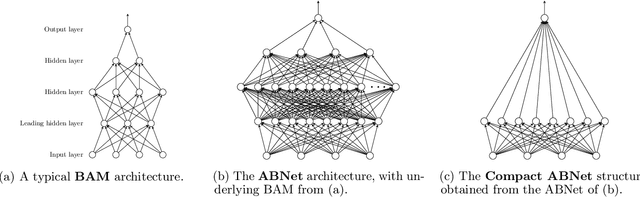
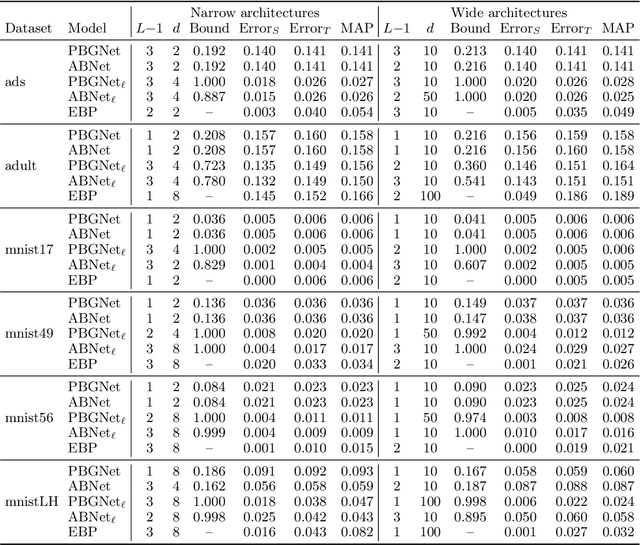
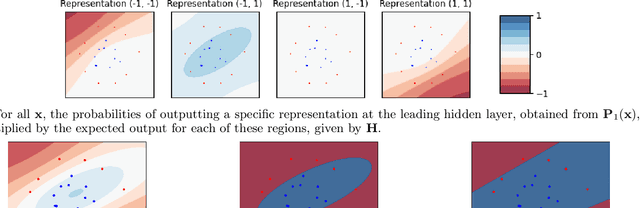
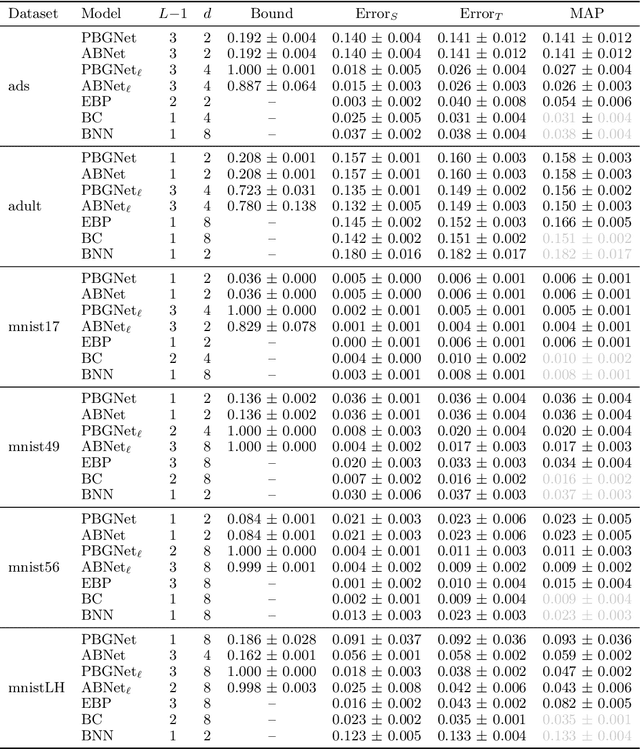
Considering a probability distribution over parameters is known as an efficient strategy to learn a neural network with non-differentiable activation functions. We study the expectation of a probabilistic neural network as a predictor by itself, focusing on the aggregation of binary activated neural networks with normal distributions over real-valued weights. Our work leverages a recent analysis derived from the PAC-Bayesian framework that derives tight generalization bounds and learning procedures for the expected output value of such an aggregation, which is given by an analytical expression. While the combinatorial nature of the latter has been circumvented by approximations in previous works, we show that the exact computation remains tractable for deep but narrow neural networks, thanks to a dynamic programming approach. This leads us to a peculiar bound minimization learning algorithm for binary activated neural networks, where the forward pass propagates probabilities over representations instead of activation values. A stochastic counterpart of this new neural networks training scheme that scales to wider architectures is proposed.

Dichotomize and Generalize: PAC-Bayesian Binary Activated Deep Neural Networks

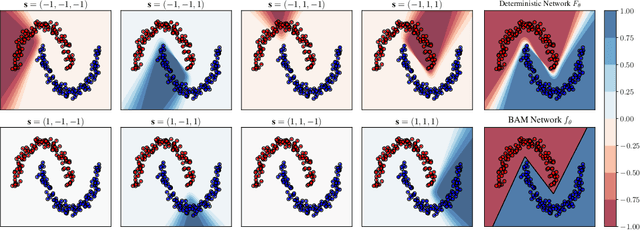
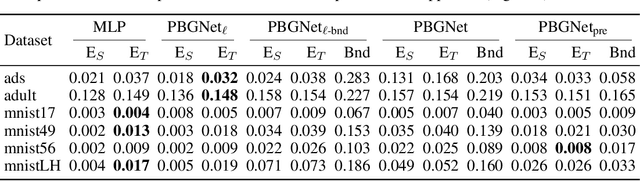
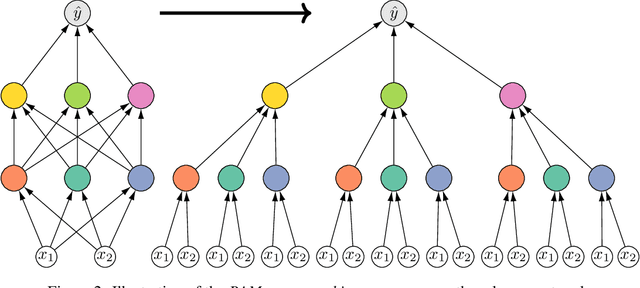
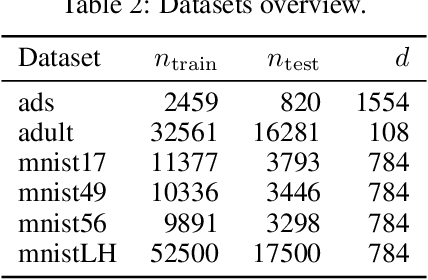
We present a comprehensive study of multilayer neural networks with binary activation, relying on the PAC-Bayesian theory. Our contributions are twofold: (i) we develop an end-to-end framework to train a binary activated deep neural network, overcoming the fact that binary activation function is non-differentiable; (ii) we provide nonvacuous PAC-Bayesian generalization bounds for binary activated deep neural networks. Noteworthy, our results are obtained by minimizing the expected loss of an architecture-dependent aggregation of binary activated deep neural networks. The performance of our approach is assessed on a thorough numerical experiment protocol on real-life datasets.

Pseudo-Bayesian Learning with Kernel Fourier Transform as Prior

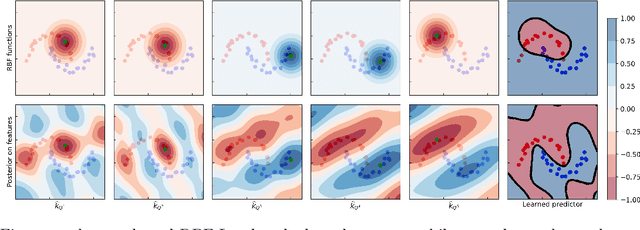
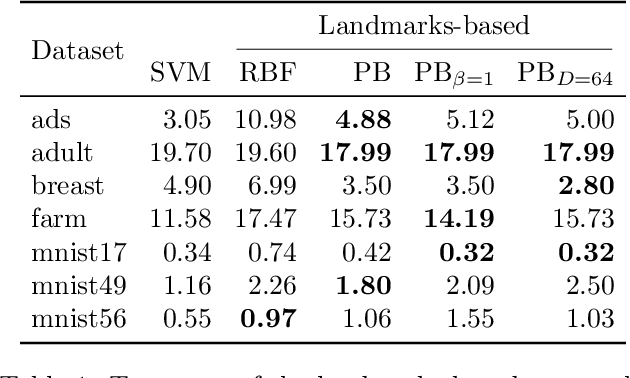
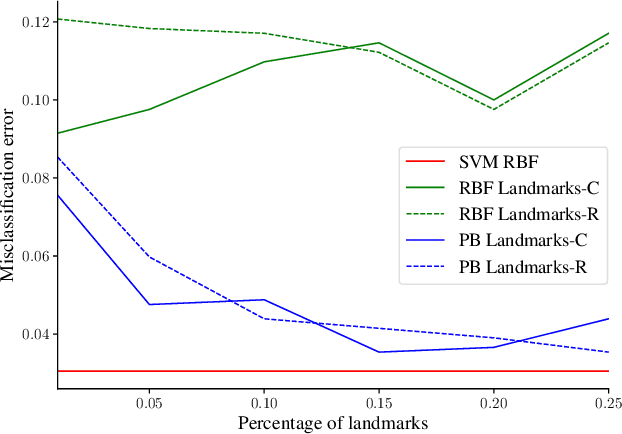
We revisit Rahimi and Recht (2007)'s kernel random Fourier features (RFF) method through the lens of the PAC-Bayesian theory. While the primary goal of RFF is to approximate a kernel, we look at the Fourier transform as a prior distribution over trigonometric hypotheses. It naturally suggests learning a posterior on these hypotheses. We derive generalization bounds that are optimized by learning a pseudo-posterior obtained from a closed-form expression. Based on this study, we consider two learning strategies: The first one finds a compact landmarks-based representation of the data where each landmark is given by a distribution-tailored similarity measure, while the second one provides a PAC-Bayesian justification to the kernel alignment method of Sinha and Duchi (2016).