Dichotomize and Generalize: PAC-Bayesian Binary Activated Deep Neural Networks
Paper and Code
May 29, 2019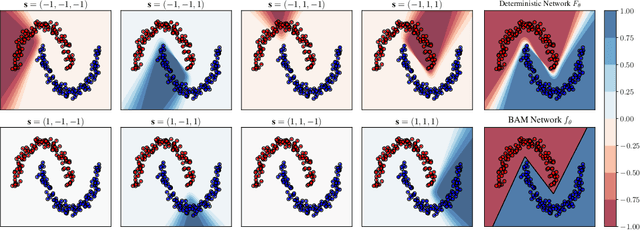
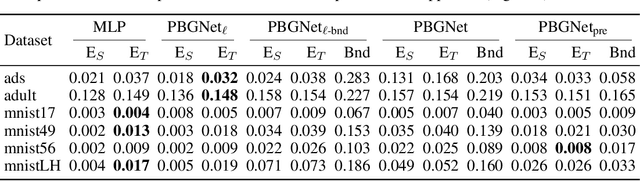
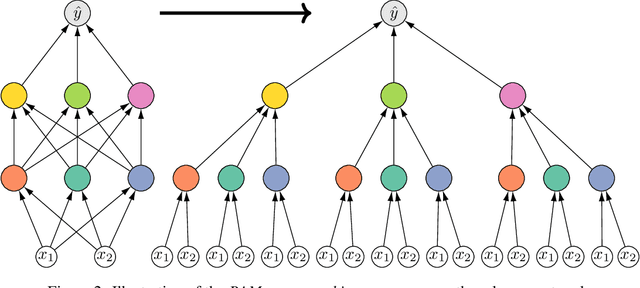
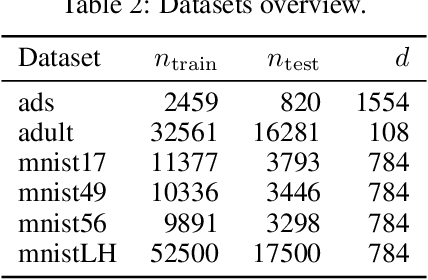
We present a comprehensive study of multilayer neural networks with binary activation, relying on the PAC-Bayesian theory. Our contributions are twofold: (i) we develop an end-to-end framework to train a binary activated deep neural network, overcoming the fact that binary activation function is non-differentiable; (ii) we provide nonvacuous PAC-Bayesian generalization bounds for binary activated deep neural networks. Noteworthy, our results are obtained by minimizing the expected loss of an architecture-dependent aggregation of binary activated deep neural networks. The performance of our approach is assessed on a thorough numerical experiment protocol on real-life datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge