Goal-Reaching Trajectory Design Near Danger with Piecewise Affine Reach-avoid Computation

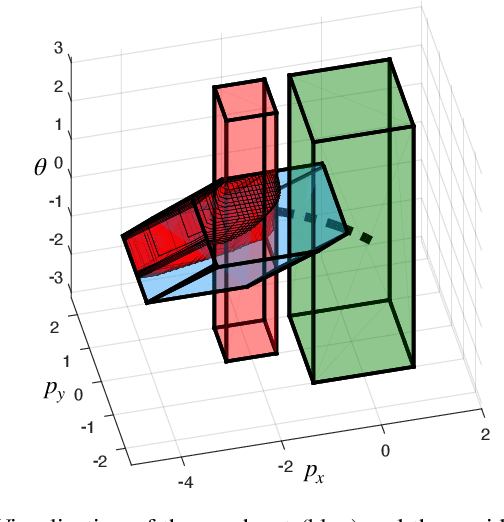
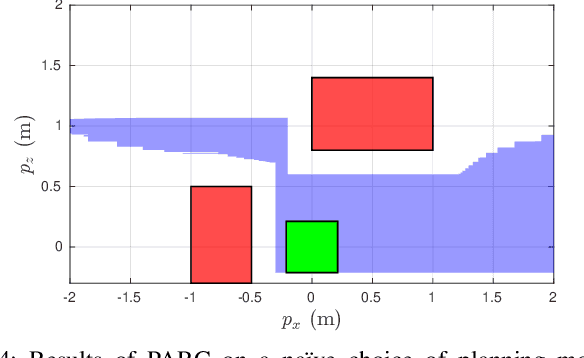
Autonomous mobile robots must maintain safety, but should not sacrifice performance, leading to the classical reach-avoid problem. This paper seeks to compute trajectory plans for which a robot is guaranteed to reach a goal and avoid obstacles in the specific near-danger case that the obstacles and goal are near each other. The proposed method builds off of a common approach of using a simplified planning model to generate plans, which are then tracked using a high-fidelity tracking model and controller. Existing safe planning approaches use reachability analysis to overapproximate the error between these models, but this introduces additional numerical approximation error and thereby conservativeness that prevents goal-reaching. The present work instead proposes a Piecewise Affine Reach-avoid Computation (PARC) method to tightly approximate the reachable set of the planning model. With PARC, the main source of conservativeness is the model mismatch, which can be mitigated by careful controller and planning model design. The utility of this method is demonstrated through extensive numerical experiments in which PARC outperforms state-of-the-art reach-avoid methods in near-danger goal-reaching. Furthermore, in a simulated demonstration, PARC enables the generation of provably-safe extreme vehicle dynamics drift parking maneuvers.

Constrained Feedforward Neural Network Training via Reachability Analysis

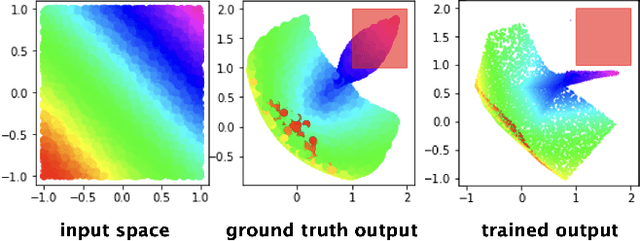
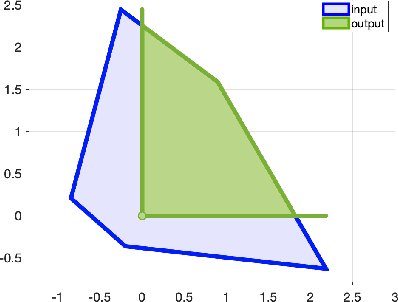
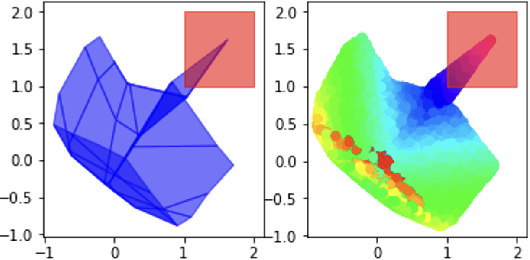
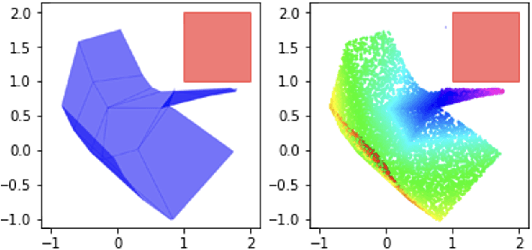
Neural networks have recently become popular for a wide variety of uses, but have seen limited application in safety-critical domains such as robotics near and around humans. This is because it remains an open challenge to train a neural network to obey safety constraints. Most existing safety-related methods only seek to verify that already-trained networks obey constraints, requiring alternating training and verification. Instead, this work proposes a constrained method to simultaneously train and verify a feedforward neural network with rectified linear unit (ReLU) nonlinearities. Constraints are enforced by computing the network's output-space reachable set and ensuring that it does not intersect with unsafe sets; training is achieved by formulating a novel collision-check loss function between the reachable set and unsafe portions of the output space. The reachable and unsafe sets are represented by constrained zonotopes, a convex polytope representation that enables differentiable collision checking. The proposed method is demonstrated successfully on a network with one nonlinearity layer and approximately 50 parameters.