Wavelet Packet Power Spectrum Kullback-Leibler Divergence: A New Metric for Image Synthesis

Current metrics for generative neural networks are biased towards low frequencies, specific generators, objects from the ImageNet dataset, and value texture more than shape. Many current quality metrics do not measure frequency information directly. In response, we propose a new frequency band-based quality metric, which opens a door into the frequency domain yet, at the same time, preserves spatial aspects of the data. Our metric works well even if the distributions we compare are far from ImageNet or have been produced by differing generator architectures. We verify the quality of our metric by sampling a broad selection of generative networks on a wide variety of data sets. A user study ensures our metric aligns with human perception. Furthermore, we show that frequency band guidance can improve the frequency domain fidelity of a current generative network.

A Benchmark for Out of Distribution Detection in Point Cloud 3D Semantic Segmentation

Safety-critical applications like autonomous driving use Deep Neural Networks (DNNs) for object detection and segmentation. The DNNs fail to predict when they observe an Out-of-Distribution (OOD) input leading to catastrophic consequences. Existing OOD detection methods were extensively studied for image inputs but have not been explored much for LiDAR inputs. So in this study, we proposed two datasets for benchmarking OOD detection in 3D semantic segmentation. We used Maximum Softmax Probability and Entropy scores generated using Deep Ensembles and Flipout versions of RandLA-Net as OOD scores. We observed that Deep Ensembles out perform Flipout model in OOD detection with greater AUROC scores for both datasets.

Canonical convolutional neural networks

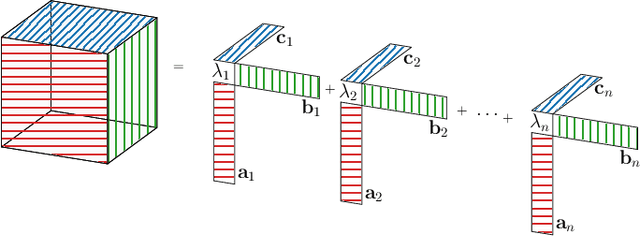
We introduce canonical weight normalization for convolutional neural networks. Inspired by the canonical tensor decomposition, we express the weight tensors in so-called canonical networks as scaled sums of outer vector products. In particular, we train network weights in the decomposed form, where scale weights are optimized separately for each mode. Additionally, similarly to weight normalization, we include a global scaling parameter. We study the initialization of the canonical form by running the power method and by drawing randomly from Gaussian or uniform distributions. Our results indicate that we can replace the power method with cheaper initializations drawn from standard distributions. The canonical re-parametrization leads to competitive normalization performance on the MNIST, CIFAR10, and SVHN data sets. Moreover, the formulation simplifies network compression. Once training has converged, the canonical form allows convenient model-compression by truncating the parameter sums.