Canonical convolutional neural networks
Paper and Code
Jun 03, 2022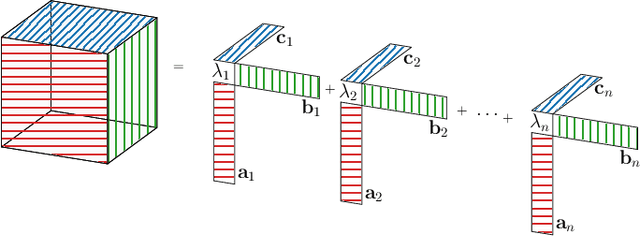



We introduce canonical weight normalization for convolutional neural networks. Inspired by the canonical tensor decomposition, we express the weight tensors in so-called canonical networks as scaled sums of outer vector products. In particular, we train network weights in the decomposed form, where scale weights are optimized separately for each mode. Additionally, similarly to weight normalization, we include a global scaling parameter. We study the initialization of the canonical form by running the power method and by drawing randomly from Gaussian or uniform distributions. Our results indicate that we can replace the power method with cheaper initializations drawn from standard distributions. The canonical re-parametrization leads to competitive normalization performance on the MNIST, CIFAR10, and SVHN data sets. Moreover, the formulation simplifies network compression. Once training has converged, the canonical form allows convenient model-compression by truncating the parameter sums.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge