Correct and Certify: A New Approach to Self-Supervised 3D-Object Perception

We consider an object pose estimation and model fitting problem, where - given a partial point cloud of an object - the goal is to estimate the object pose by fitting a CAD model to the sensor data. We solve this problem by combining (i) a semantic keypoint-based pose estimation model, (ii) a novel self-supervised training approach, and (iii) a certification procedure, that not only verifies whether the output produced by the model is correct or not, but also flags uniqueness of the produced solution. The semantic keypoint detector model is initially trained in simulation and does not perform well on real-data due to the domain gap. Our self-supervised training procedure uses a corrector and a certification module to improve the detector. The corrector module corrects the detected keypoints to compensate for the domain gap, and is implemented as a declarative layer, for which we develop a simple differentiation rule. The certification module declares whether the corrected output produced by the model is certifiable (i.e. correct) or not. At each iteration, the approach optimizes over the loss induced only by the certifiable input-output pairs. As training progresses, we see that the fraction of outputs that are certifiable increases, eventually reaching near $100\%$ in many cases. We also introduce the notion of strong certifiability wherein the model can determine if the predicted object model fit is unique or not. The detected semantic keypoints help us implement this in the forward pass. We conduct extensive experiments to evaluate the performance of the corrector, the certification, and the proposed self-supervised training using the ShapeNet and YCB datasets, and show the proposed approach achieves performance comparable to fully supervised baselines while not requiring pose or keypoint supervision on real data.

Hierarchical Representations and Explicit Memory: Learning Effective Navigation Policies on 3D Scene Graphs using Graph Neural Networks

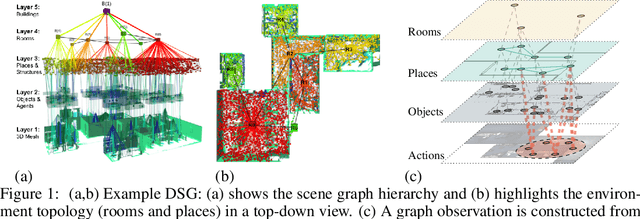
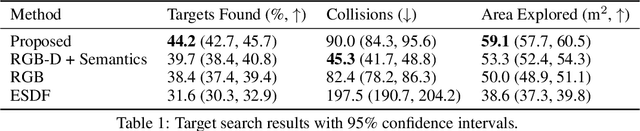
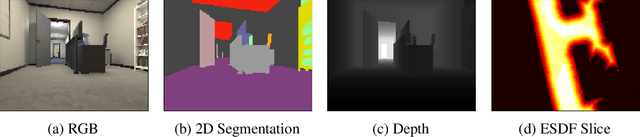
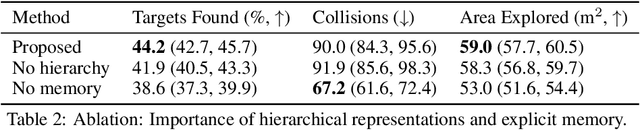
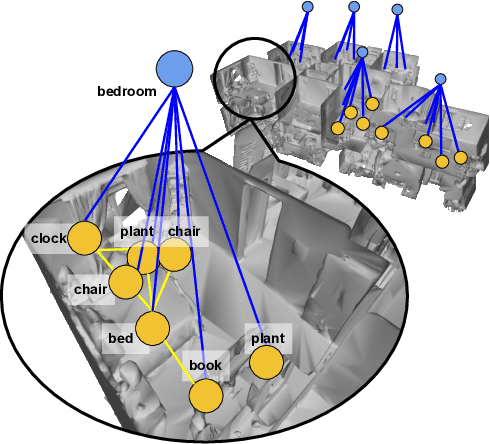
Representations are crucial for a robot to learn effective navigation policies. Recent work has shown that mid-level perceptual abstractions, such as depth estimates or 2D semantic segmentation, lead to more effective policies when provided as observations in place of raw sensor data (e.g., RGB images). However, such policies must still learn latent three-dimensional scene properties from mid-level abstractions. In contrast, high-level, hierarchical representations such as 3D scene graphs explicitly provide a scene's geometry, topology, and semantics, making them compelling representations for navigation. In this work, we present a reinforcement learning framework that leverages high-level hierarchical representations to learn navigation policies. Towards this goal, we propose a graph neural network architecture and show how to embed a 3D scene graph into an agent-centric feature space, which enables the robot to learn policies for low-level action in an end-to-end manner. For each node in the scene graph, our method uses features that capture occupancy and semantic content, while explicitly retaining memory of the robot trajectory. We demonstrate the effectiveness of our method against commonly used visuomotor policies in a challenging object search task. These experiments and supporting ablation studies show that our method leads to more effective object search behaviors, exhibits improved long-term memory, and successfully leverages hierarchical information to guide its navigation objectives.

Neural Trees for Learning on Graphs

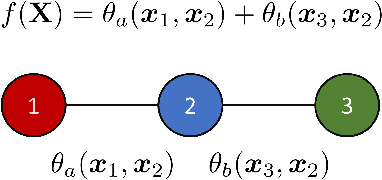
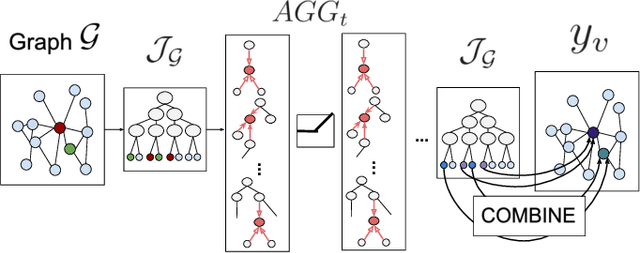
Graph Neural Networks (GNNs) have emerged as a flexible and powerful approach for learning over graphs. Despite this success, existing GNNs are constrained by their local message-passing architecture and are provably limited in their expressive power. In this work, we propose a new GNN architecture -- the Neural Tree. The neural tree architecture does not perform message passing on the input graph but on a tree-structured graph, called the H-tree, that is constructed from the input graph. Nodes in the H-tree correspond to subgraphs in the input graph, and they are reorganized in a hierarchical manner such that a parent-node of a node in the H-tree always corresponds to a larger subgraph in the input graph. We show that the neural tree architecture can approximate any smooth probability distribution function over an undirected graph, as well as emulate the junction tree algorithm. We also prove that the number of parameters needed to achieve an $\epsilon$-approximation of the distribution function is exponential in the treewidth of the input graph, but linear in its size. We apply the neural tree to semi-supervised node classification in 3D scene graphs, and show that these theoretical properties translate into significant gains in prediction accuracy, over the more traditional GNN architectures.