Linfang Hou
Data-Efficient Reinforcement Learning for Malaria Control
May 05, 2021



Abstract:Sequential decision-making under cost-sensitive tasks is prohibitively daunting, especially for the problem that has a significant impact on people's daily lives, such as malaria control, treatment recommendation. The main challenge faced by policymakers is to learn a policy from scratch by interacting with a complex environment in a few trials. This work introduces a practical, data-efficient policy learning method, named Variance-Bonus Monte Carlo Tree Search~(VB-MCTS), which can copy with very little data and facilitate learning from scratch in only a few trials. Specifically, the solution is a model-based reinforcement learning method. To avoid model bias, we apply Gaussian Process~(GP) regression to estimate the transitions explicitly. With the GP world model, we propose a variance-bonus reward to measure the uncertainty about the world. Adding the reward to the planning with MCTS can result in more efficient and effective exploration. Furthermore, the derived polynomial sample complexity indicates that VB-MCTS is sample efficient. Finally, outstanding performance on a competitive world-level RL competition and extensive experimental results verify its advantage over the state-of-the-art on the challenging malaria control task.
Robust Reinforcement Learning with Wasserstein Constraint
Jun 01, 2020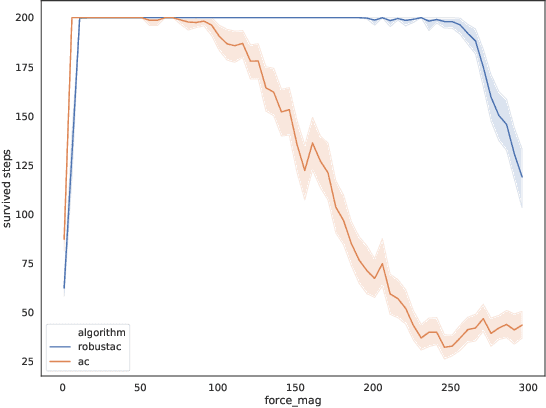
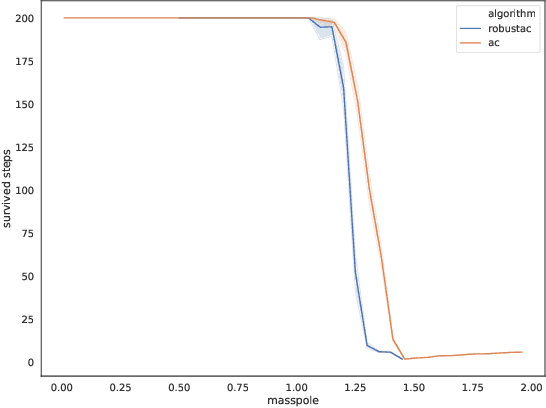
Abstract:Robust Reinforcement Learning aims to find the optimal policy with some extent of robustness to environmental dynamics. Existing learning algorithms usually enable the robustness through disturbing the current state or simulating environmental parameters in a heuristic way, which lack quantified robustness to the system dynamics (i.e. transition probability). To overcome this issue, we leverage Wasserstein distance to measure the disturbance to the reference transition kernel. With Wasserstein distance, we are able to connect transition kernel disturbance to the state disturbance, i.e. reduce an infinite-dimensional optimization problem to a finite-dimensional risk-aware problem. Through the derived risk-aware optimal Bellman equation, we show the existence of optimal robust policies, provide a sensitivity analysis for the perturbations, and then design a novel robust learning algorithm--Wasserstein Robust Advantage Actor-Critic algorithm (WRAAC). The effectiveness of the proposed algorithm is verified in the Cart-Pole environment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge