An Equivalent Graph Reconstruction Model and its Application in Recommendation Prediction

Recommendation algorithm plays an important role in recommendation system (RS), which predicts users' interests and preferences for some given items based on their known information. Recently, a recommendation algorithm based on the graph Laplacian regularization was proposed, which treats the prediction problem of the recommendation system as a reconstruction issue of small samples of the graph signal under the same graph model. Such a technique takes into account both known and unknown labeled samples information, thereby obtaining good prediction accuracy. However, when the data size is large, solving the reconstruction model is computationally expensive even with an approximate strategy. In this paper, we propose an equivalent reconstruction model that can be solved exactly with extremely low computational cost. Finally, a final prediction algorithm is proposed. We find in the experiments that the proposed method significantly reduces the computational cost while maintaining a good prediction accuracy.

Perfect Reconstruction Two-Channel Filter Banks on Arbitrary Graphs

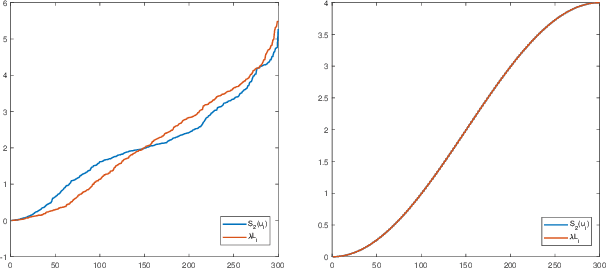
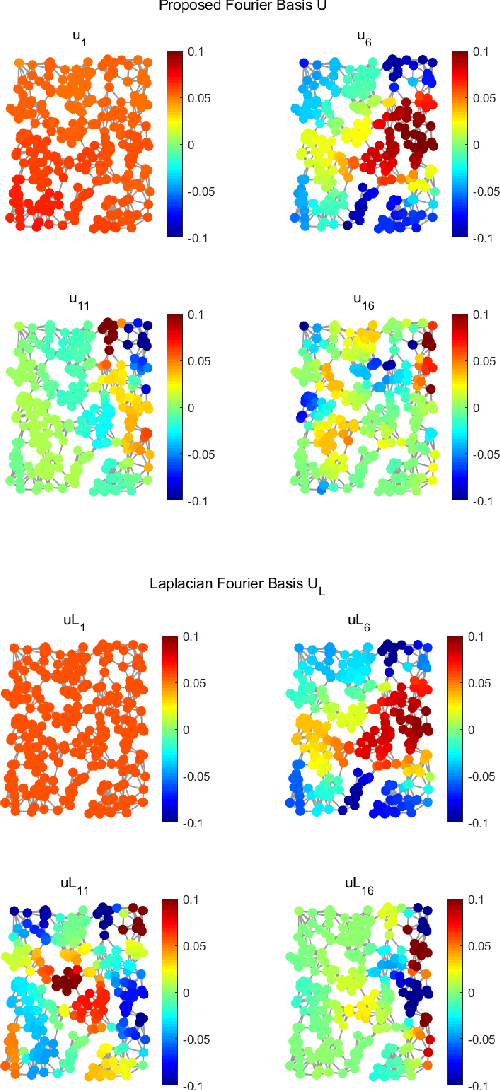
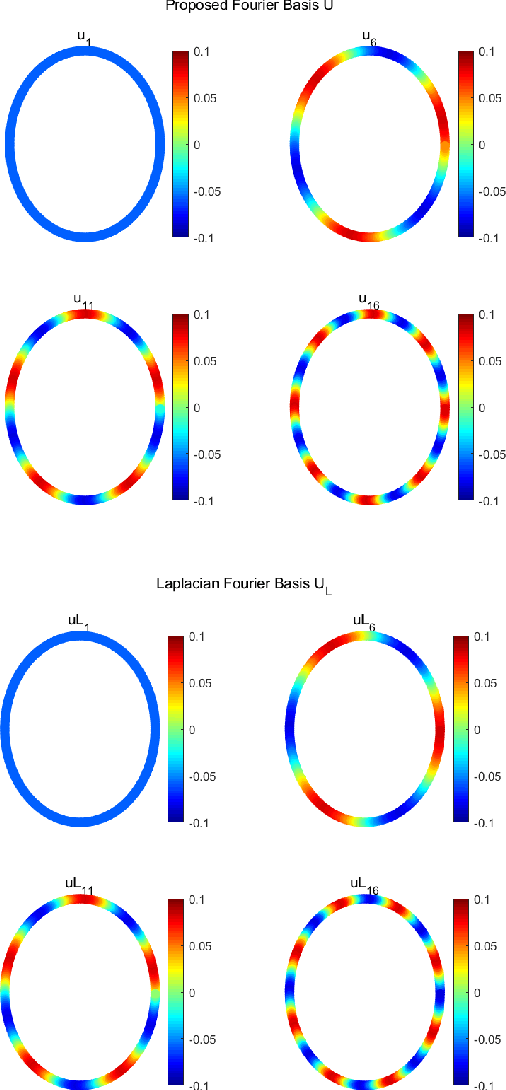
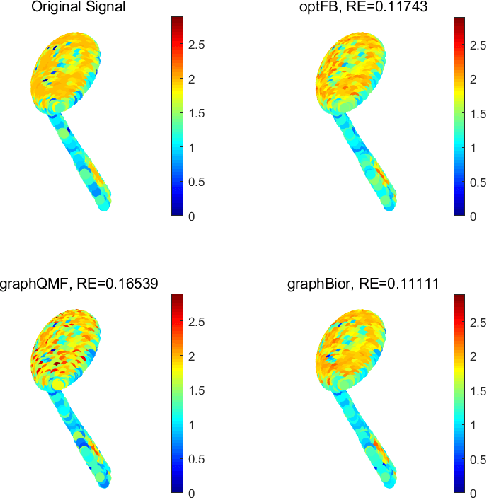
This paper extends the existing theory of perfect reconstruction two-channel filter banks from bipartite graphs to non-bipartite graphs. By generalizing the concept of downsampling/upsampling we establish the frame of two-channel filter bank on arbitrary connected, undirected and weighted graphs. Then the equations for perfect reconstruction of the filter banks are presented and solved under proper conditions. Algorithms for designing orthogonal and biorthogonal banks are given and two typical orthogonal two-channel filter banks are calculated. The locality and approximation properties of such filter banks are discussed theoretically and experimentally.

Spline-Like Wavelet Filterbanks with Perfect Reconstruction on Arbitrary Graphs

In this work, we propose a class of spline-like wavelet filterbanks for graph signals. These filterbanks possess the properties of critical sampling and perfect reconstruction. Besides, the analysis filters are localized in the graph domain because they are polynomials of the normalized adjacency matrix of the graph. We generalize the spline-like filters in the literature so that they have the ability to annihilate signals of some specified frequencies. Optimization problems are posed for the analysis filters to approximate desired responses. We conduct some experiments to demonstrate the good locality of the proposed filters and the good performance of the filterbank in the denoising task.

Perfect Reconstruction Two-Channel Filter Banks on Arbitrary Graphs Based on an Optimization Model

In this paper, we propose the construction of critically sampled perfect reconstruction two-channel filterbanks on arbitrary undirected graphs.Inspired by the design of graphQMF proposed in the literature, we propose a general ``spectral folding property'' similar to that of bipartite graphs and provide sufficient conditions for constructing perfect reconstruction filterbanks based on a general graph Fourier basis, which is not the eigenvectors of the Laplacian matrix. To obtain the desired graph Fourier basis, we need to solve a series of quadratic equality constrained quadratic optimization problems (QECQPs) which are known to be non-convex and difficult to solve. We develop an algorithm to obtain the global optimal solution within a pre-specified tolerance. Multi-resolution analysis on real-world data and synthetic data are performed to validate the effectiveness of the proposed filterbanks.

Atomic Filter: a Weak Form of Shift Operator for Graph Signals

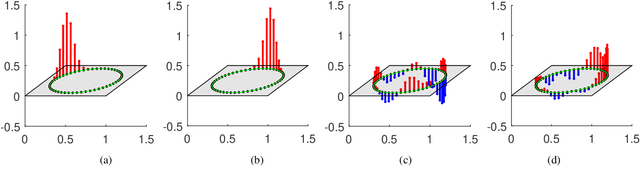
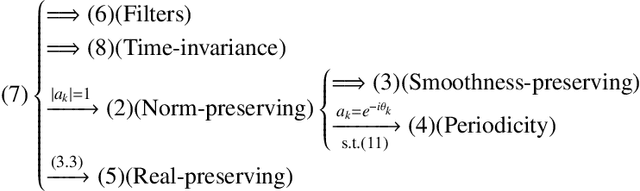
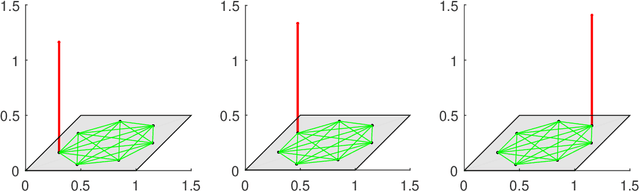
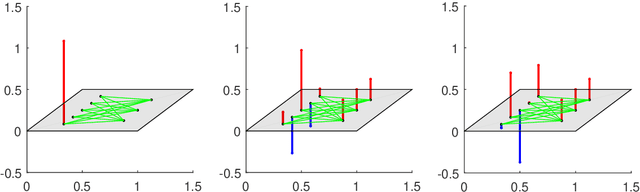
The shift operation plays a crucial role in the classical signal processing. It is the generator of all the filters and the basic operation for time-frequency analysis, such as windowed Fourier transform and wavelet transform. With the rapid development of internet technology and big data science, a large amount of data are expressed as signals defined on graphs. In order to establish the theory of filtering, windowed Fourier transform and wavelet transform in the setting of graph signals, we need to extend the shift operation of classical signals to graph signals. It is a fundamental problem since the vertex set of a graph is usually not a vector space and the addition operation cannot be defined on the vertex set of the graph. In this paper, based on our understanding on the core role of shift operation in classical signal processing we propose the concept of atomic filters, which can be viewed as a weak form of the shift operator for graph signals. Then, we study the conditions such that an atomic filter is norm-preserving, periodic, or real-preserving. The property of real-preserving holds naturally in the classical signal processing, but no the research has been reported on this topic in the graph signal setting. With these conditions we propose the concept of normal atomic filters for graph signals, which degenerates into the classical shift operator under mild conditions if the graph is circulant. Typical examples of graphs that have or have not normal atomic filters are given. Finally, as an application, atomic filters are utilized to construct time-frequency atoms which constitute a frame of the graph signal space.