Perfect Reconstruction Two-Channel Filter Banks on Arbitrary Graphs Based on an Optimization Model
Paper and Code
Aug 04, 2022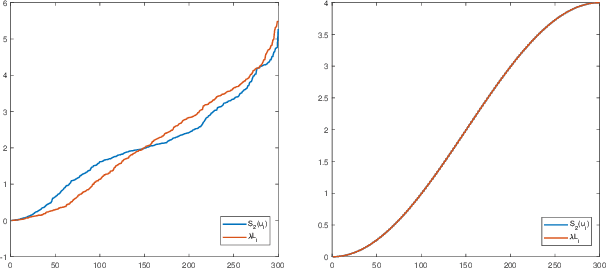
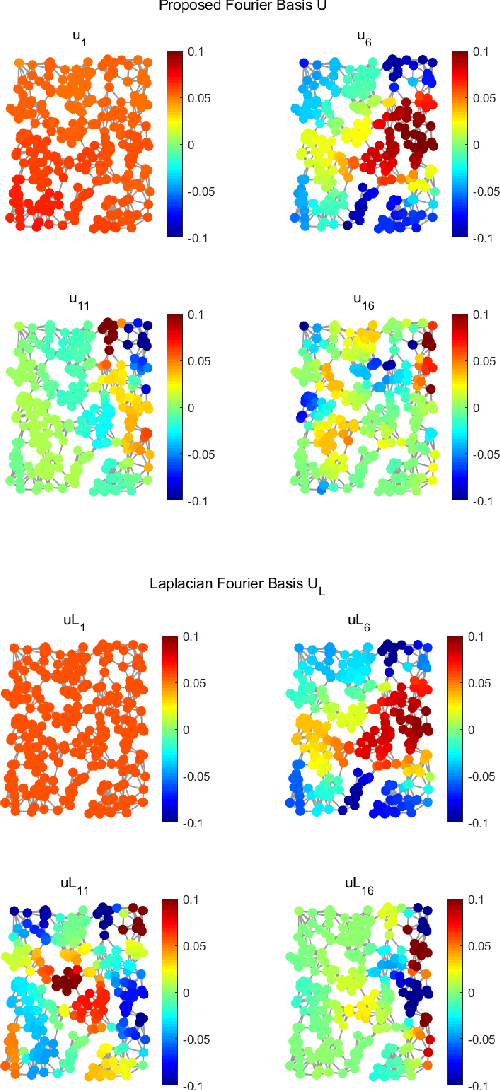
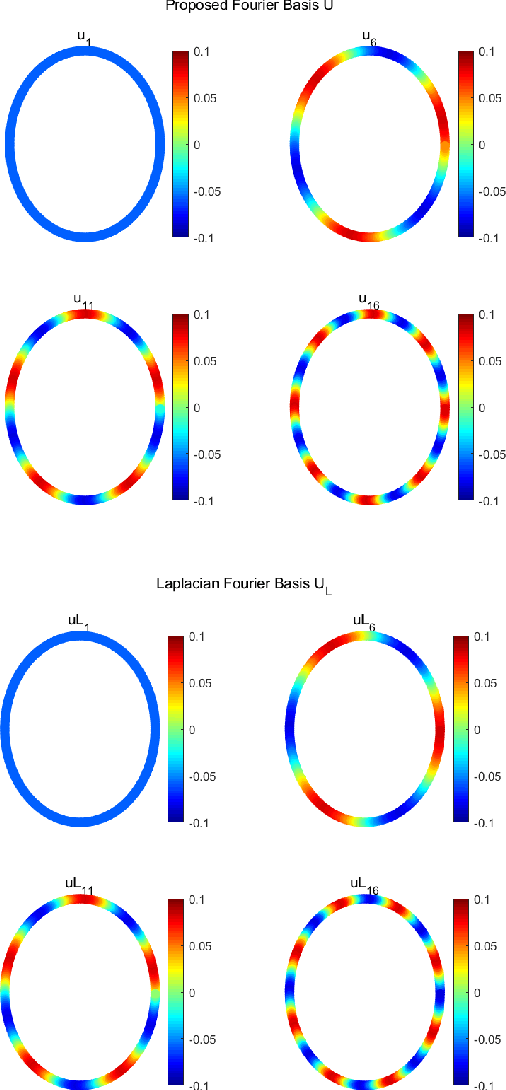
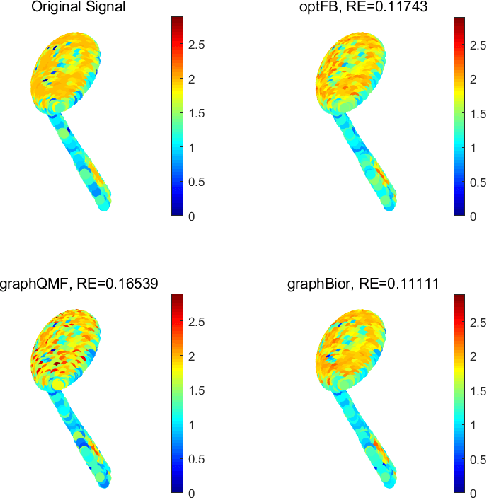
In this paper, we propose the construction of critically sampled perfect reconstruction two-channel filterbanks on arbitrary undirected graphs.Inspired by the design of graphQMF proposed in the literature, we propose a general ``spectral folding property'' similar to that of bipartite graphs and provide sufficient conditions for constructing perfect reconstruction filterbanks based on a general graph Fourier basis, which is not the eigenvectors of the Laplacian matrix. To obtain the desired graph Fourier basis, we need to solve a series of quadratic equality constrained quadratic optimization problems (QECQPs) which are known to be non-convex and difficult to solve. We develop an algorithm to obtain the global optimal solution within a pre-specified tolerance. Multi-resolution analysis on real-world data and synthetic data are performed to validate the effectiveness of the proposed filterbanks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge