Perfect Reconstruction Two-Channel Filter Banks on Arbitrary Graphs

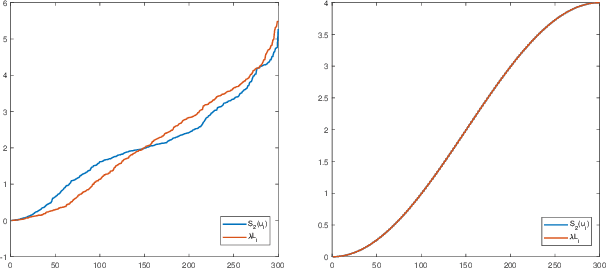
This paper extends the existing theory of perfect reconstruction two-channel filter banks from bipartite graphs to non-bipartite graphs. By generalizing the concept of downsampling/upsampling we establish the frame of two-channel filter bank on arbitrary connected, undirected and weighted graphs. Then the equations for perfect reconstruction of the filter banks are presented and solved under proper conditions. Algorithms for designing orthogonal and biorthogonal banks are given and two typical orthogonal two-channel filter banks are calculated. The locality and approximation properties of such filter banks are discussed theoretically and experimentally.

Spline-Like Wavelet Filterbanks with Perfect Reconstruction on Arbitrary Graphs

In this work, we propose a class of spline-like wavelet filterbanks for graph signals. These filterbanks possess the properties of critical sampling and perfect reconstruction. Besides, the analysis filters are localized in the graph domain because they are polynomials of the normalized adjacency matrix of the graph. We generalize the spline-like filters in the literature so that they have the ability to annihilate signals of some specified frequencies. Optimization problems are posed for the analysis filters to approximate desired responses. We conduct some experiments to demonstrate the good locality of the proposed filters and the good performance of the filterbank in the denoising task.

Perfect Reconstruction Two-Channel Filter Banks on Arbitrary Graphs Based on an Optimization Model

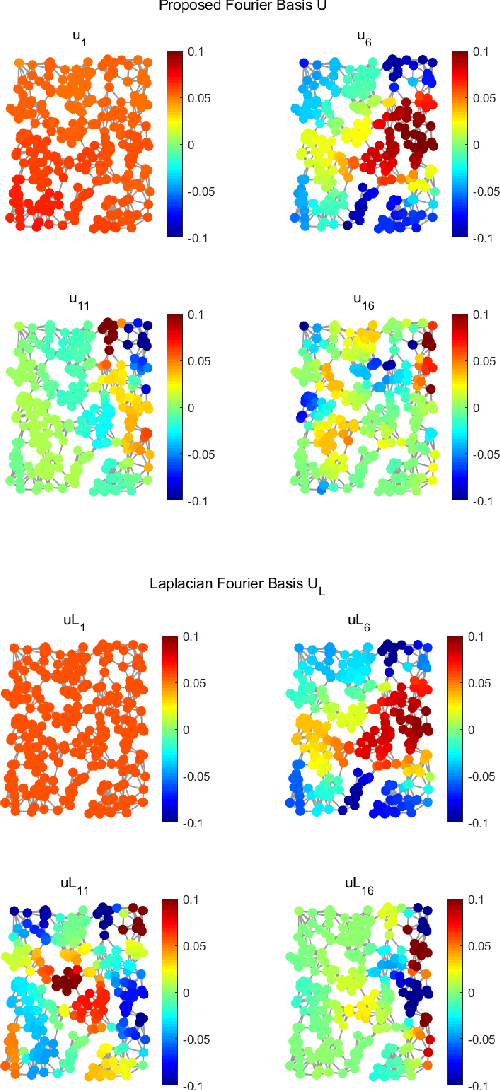
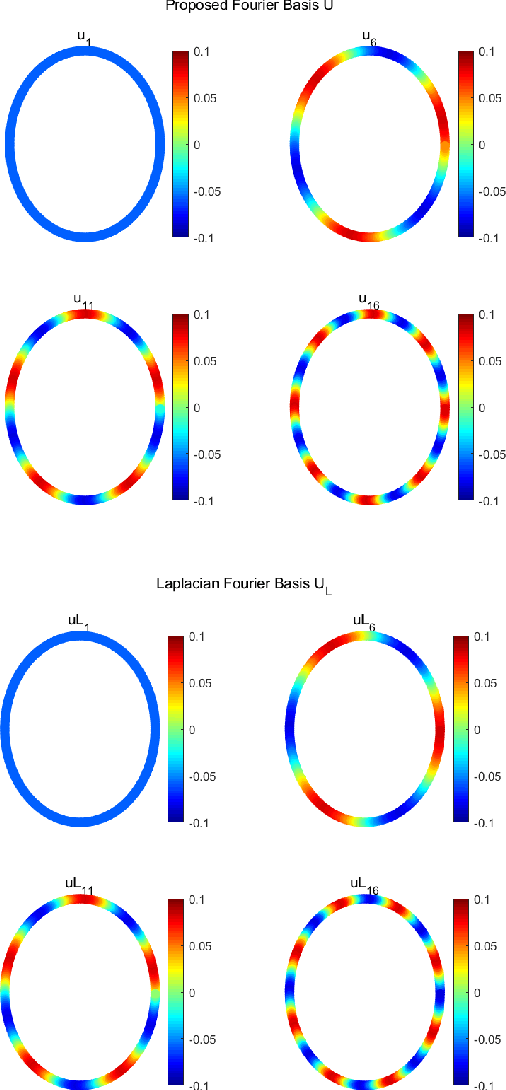
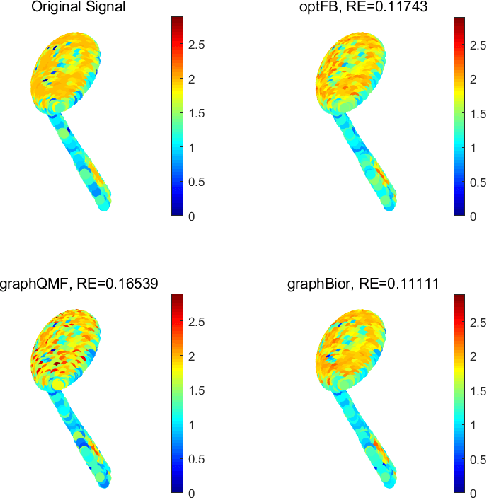
In this paper, we propose the construction of critically sampled perfect reconstruction two-channel filterbanks on arbitrary undirected graphs.Inspired by the design of graphQMF proposed in the literature, we propose a general ``spectral folding property'' similar to that of bipartite graphs and provide sufficient conditions for constructing perfect reconstruction filterbanks based on a general graph Fourier basis, which is not the eigenvectors of the Laplacian matrix. To obtain the desired graph Fourier basis, we need to solve a series of quadratic equality constrained quadratic optimization problems (QECQPs) which are known to be non-convex and difficult to solve. We develop an algorithm to obtain the global optimal solution within a pre-specified tolerance. Multi-resolution analysis on real-world data and synthetic data are performed to validate the effectiveness of the proposed filterbanks.