Perfect Reconstruction Two-Channel Filter Banks on Arbitrary Graphs
Paper and Code
Oct 05, 2022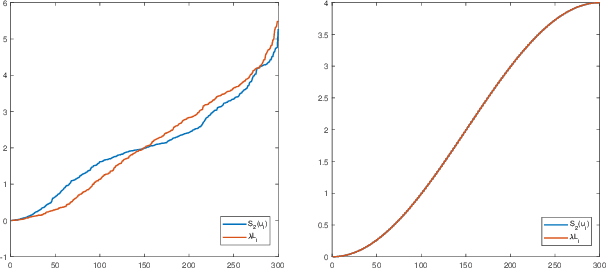
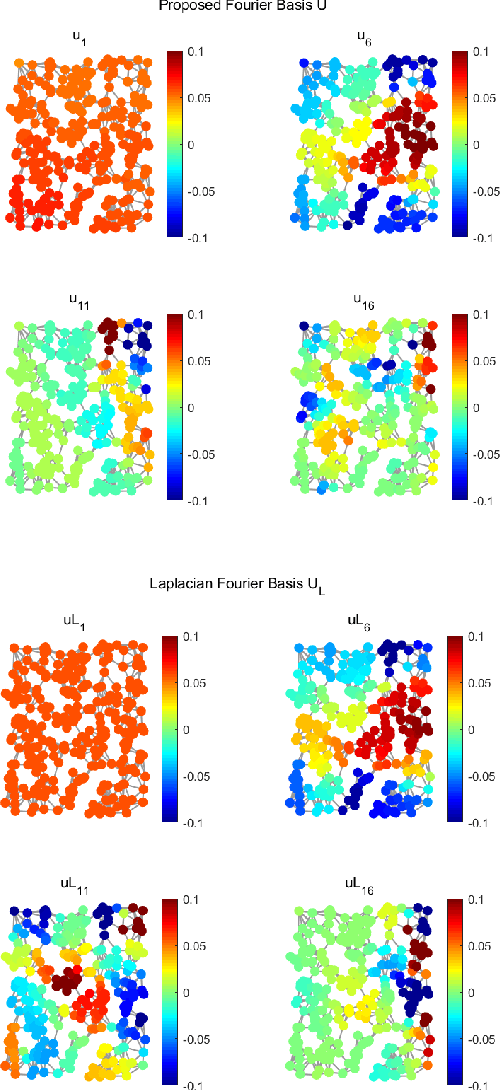
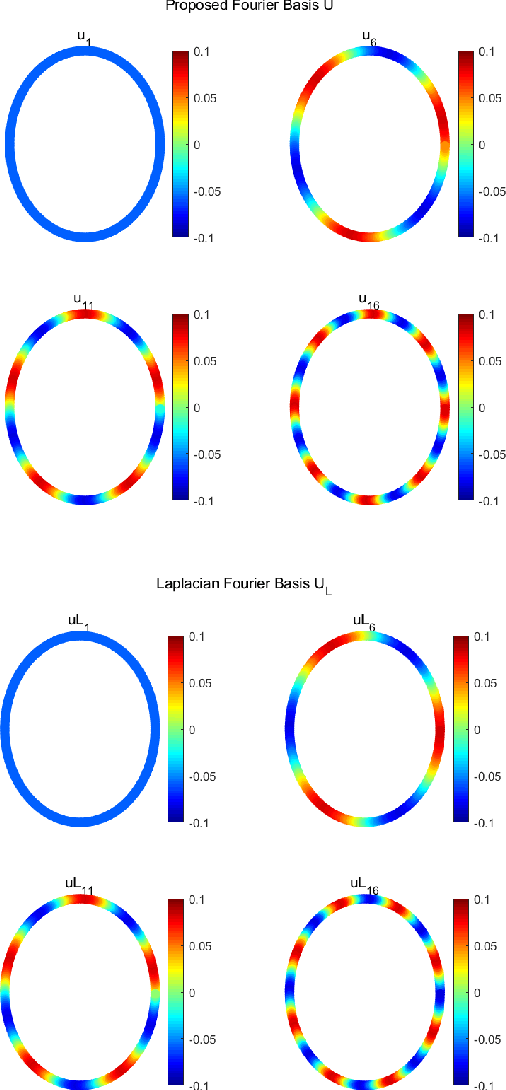
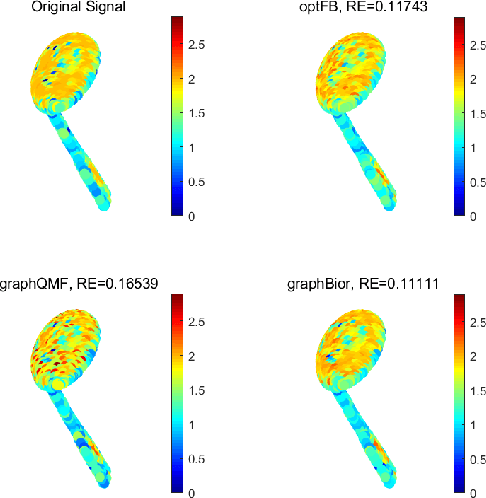
This paper extends the existing theory of perfect reconstruction two-channel filter banks from bipartite graphs to non-bipartite graphs. By generalizing the concept of downsampling/upsampling we establish the frame of two-channel filter bank on arbitrary connected, undirected and weighted graphs. Then the equations for perfect reconstruction of the filter banks are presented and solved under proper conditions. Algorithms for designing orthogonal and biorthogonal banks are given and two typical orthogonal two-channel filter banks are calculated. The locality and approximation properties of such filter banks are discussed theoretically and experimentally.
* 33 pages,11 figures. This manuscript has been submitted to
ScienceDirect Applied and Computational Harmonic Analysis (ACHA) on Jan
27,2022
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge