Atomic Filter: a Weak Form of Shift Operator for Graph Signals

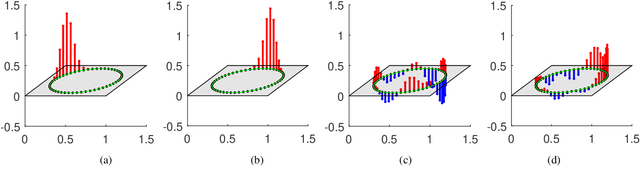
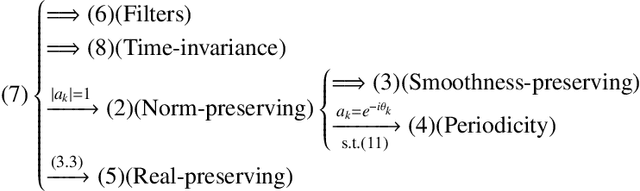
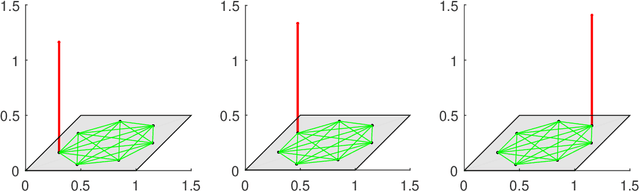
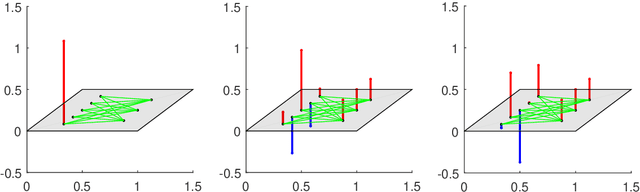
The shift operation plays a crucial role in the classical signal processing. It is the generator of all the filters and the basic operation for time-frequency analysis, such as windowed Fourier transform and wavelet transform. With the rapid development of internet technology and big data science, a large amount of data are expressed as signals defined on graphs. In order to establish the theory of filtering, windowed Fourier transform and wavelet transform in the setting of graph signals, we need to extend the shift operation of classical signals to graph signals. It is a fundamental problem since the vertex set of a graph is usually not a vector space and the addition operation cannot be defined on the vertex set of the graph. In this paper, based on our understanding on the core role of shift operation in classical signal processing we propose the concept of atomic filters, which can be viewed as a weak form of the shift operator for graph signals. Then, we study the conditions such that an atomic filter is norm-preserving, periodic, or real-preserving. The property of real-preserving holds naturally in the classical signal processing, but no the research has been reported on this topic in the graph signal setting. With these conditions we propose the concept of normal atomic filters for graph signals, which degenerates into the classical shift operator under mild conditions if the graph is circulant. Typical examples of graphs that have or have not normal atomic filters are given. Finally, as an application, atomic filters are utilized to construct time-frequency atoms which constitute a frame of the graph signal space.