Plotting time: On the usage of CNNs for time series classification

We present a novel approach for time series classification where we represent time series data as plot images and feed them to a simple CNN, outperforming several state-of-the-art methods. We propose a simple and highly replicable way of plotting the time series, and feed these images as input to a non-optimized shallow CNN, without any normalization or residual connections. These representations are no more than default line plots using the time series data, where the only pre-processing applied is to reduce the number of white pixels in the image. We compare our method with different state-of-the-art methods specialized in time series classification on two real-world non public datasets, as well as 98 datasets of the UCR dataset collection. The results show that our approach is very promising, achieving the best results on both real-world datasets and matching / beating the best state-of-the-art methods in six UCR datasets. We argue that, if a simple naive design like ours can obtain such good results, it is worth further exploring the capabilities of using image representation of time series data, along with more powerful CNNs, for classification and other related tasks.

A Study of Fitness Landscapes for Neuroevolution

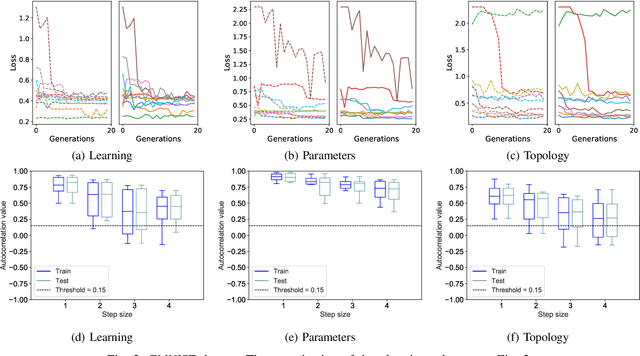
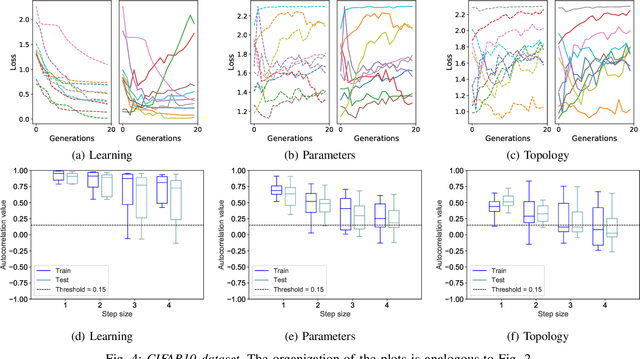
Fitness landscapes are a useful concept to study the dynamics of meta-heuristics. In the last two decades, they have been applied with success to estimate the optimization power of several types of evolutionary algorithms, including genetic algorithms and genetic programming. However, so far they have never been used to study the performance of machine learning algorithms on unseen data, and they have never been applied to neuroevolution. This paper aims at filling both these gaps, applying for the first time fitness landscapes to neuroevolution and using them to infer useful information about the predictive ability of the method. More specifically, we use a grammar-based approach to generate convolutional neural networks, and we study the dynamics of three different mutations to evolve them. To characterize fitness landscapes, we study autocorrelation and entropic measure of ruggedness. The results show that these measures are appropriate for estimating both the optimization power and the generalization ability of the considered neuroevolution configurations.

Pruning Techniques for Mixed Ensembles of Genetic Programming Models

The objective of this paper is to define an effective strategy for building an ensemble of Genetic Programming (GP) models. Ensemble methods are widely used in machine learning due to their features: they average out biases, they reduce the variance and they usually generalize better than single models. Despite these advantages, building ensemble of GP models is not a well-developed topic in the evolutionary computation community. To fill this gap, we propose a strategy that blends individuals produced by standard syntax-based GP and individuals produced by geometric semantic genetic programming, one of the newest semantics-based method developed in GP. In fact, recent literature showed that combining syntax and semantics could improve the generalization ability of a GP model. Additionally, to improve the diversity of the GP models used to build up the ensemble, we propose different pruning criteria that are based on correlation and entropy, a commonly used measure in information theory. Experimental results,obtained over different complex problems, suggest that the pruning criteria based on correlation and entropy could be effective in improving the generalization ability of the ensemble model and in reducing the computational burden required to build it.

A Distance Between Populations for n-Points Crossover in Genetic Algorithms

Genetic algorithms (GAs) are an optimization technique that has been successfully used on many real-world problems. There exist different approaches to their theoretical study. In this paper we complete a recently presented approach to model one-point crossover using pretopologies (or Cech topologies) in two ways. First, we extend it to the case of n-points crossover. Then, we experimentally study how the distance distribution changes when the number of crossover points increases.

An Efficient Genetic Programming System with Geometric Semantic Operators and its Application to Human Oral Bioavailability Prediction

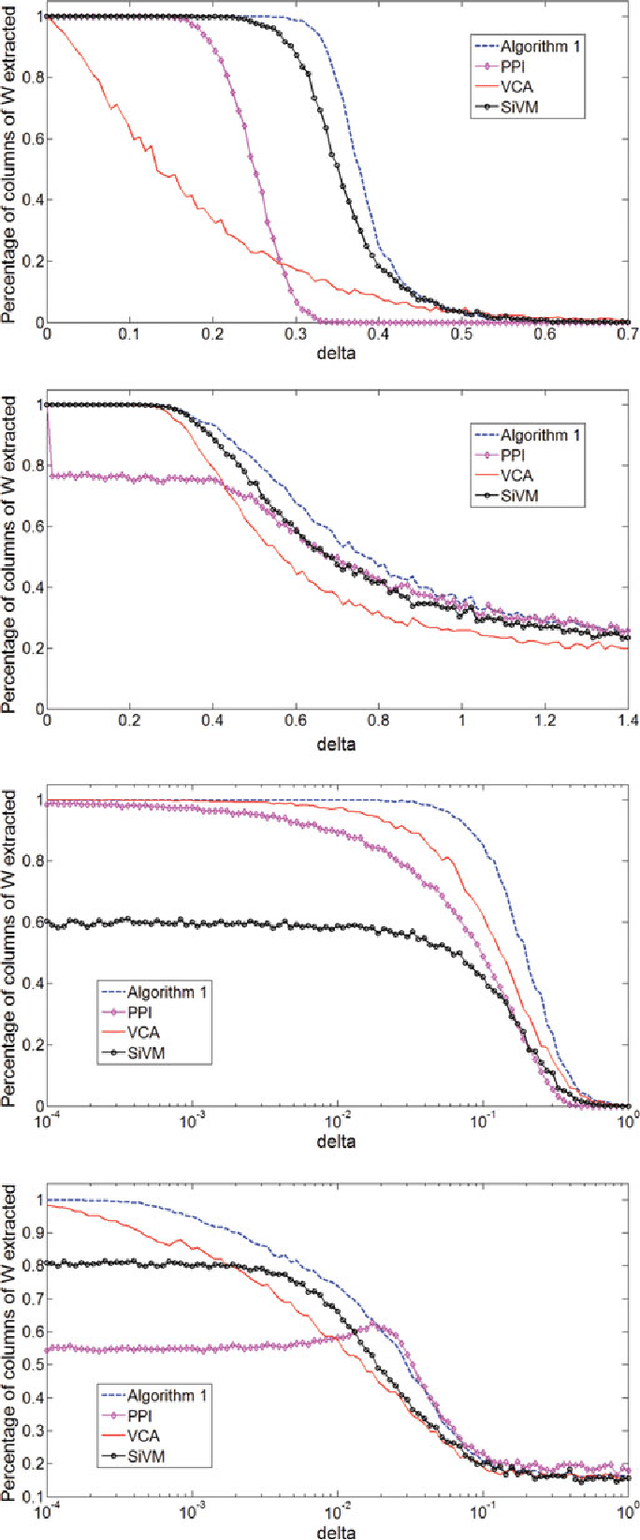
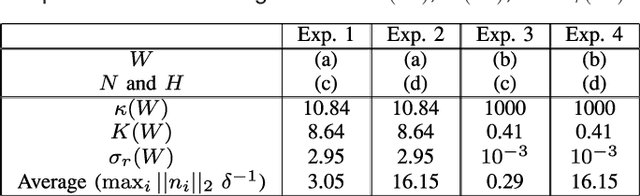
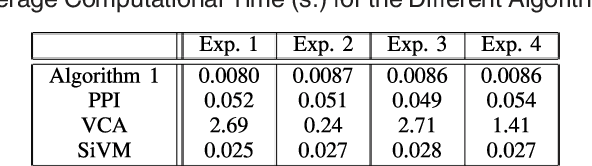
Very recently new genetic operators, called geometric semantic operators, have been defined for genetic programming. Contrarily to standard genetic operators, which are uniquely based on the syntax of the individuals, these new operators are based on their semantics, meaning with it the set of input-output pairs on training data. Furthermore, these operators present the interesting property of inducing a unimodal fitness landscape for every problem that consists in finding a match between given input and output data (for instance regression and classification). Nevertheless, the current definition of these operators has a serious limitation: they impose an exponential growth in the size of the individuals in the population, so their use is impossible in practice. This paper is intended to overcome this limitation, presenting a new genetic programming system that implements geometric semantic operators in an extremely efficient way. To demonstrate the power of the proposed system, we use it to solve a complex real-life application in the field of pharmacokinetic: the prediction of the human oral bioavailability of potential new drugs. Besides the excellent performances on training data, which were expected because the fitness landscape is unimodal, we also report an excellent generalization ability of the proposed system, at least for the studied application. In fact, it outperforms standard genetic programming and a wide set of other well-known machine learning methods.

NK landscapes difficulty and Negative Slope Coefficient: How Sampling Influences the Results

Negative Slope Coefficient is an indicator of problem hardness that has been introduced in 2004 and that has returned promising results on a large set of problems. It is based on the concept of fitness cloud and works by partitioning the cloud into a number of bins representing as many different regions of the fitness landscape. The measure is calculated by joining the bins centroids by segments and summing all their negative slopes. In this paper, for the first time, we point out a potential problem of the Negative Slope Coefficient: we study its value for different instances of the well known NK-landscapes and we show how this indicator is dramatically influenced by the minimum number of points contained into a bin. Successively, we formally justify this behavior of the Negative Slope Coefficient and we discuss pros and cons of this measure.

Neutral Fitness Landscape in the Cellular Automata Majority Problem

We study in detail the fitness landscape of a difficult cellular automata computational task: the majority problem. Our results show why this problem landscape is so hard to search, and we quantify the large degree of neutrality found in various ways. We show that a particular subspace of the solution space, called the "Olympus", is where good solutions concentrate, and give measures to quantitatively characterize this subspace.

Fitness landscape of the cellular automata majority problem: View from the Olympus

In this paper we study cellular automata (CAs) that perform the computational Majority task. This task is a good example of what the phenomenon of emergence in complex systems is. We take an interest in the reasons that make this particular fitness landscape a difficult one. The first goal is to study the landscape as such, and thus it is ideally independent from the actual heuristics used to search the space. However, a second goal is to understand the features a good search technique for this particular problem space should possess. We statistically quantify in various ways the degree of difficulty of searching this landscape. Due to neutrality, investigations based on sampling techniques on the whole landscape are difficult to conduct. So, we go exploring the landscape from the top. Although it has been proved that no CA can perform the task perfectly, several efficient CAs for this task have been found. Exploiting similarities between these CAs and symmetries in the landscape, we define the Olympus landscape which is regarded as the ''heavenly home'' of the best local optima known (blok). Then we measure several properties of this subspace. Although it is easier to find relevant CAs in this subspace than in the overall landscape, there are structural reasons that prevent a searcher from finding overfitted CAs in the Olympus. Finally, we study dynamics and performance of genetic algorithms on the Olympus in order to confirm our analysis and to find efficient CAs for the Majority problem with low computational cost.