Projected Regression Methods for Inverting Fredholm Integrals: Formalism and Application to Analytical Continuation

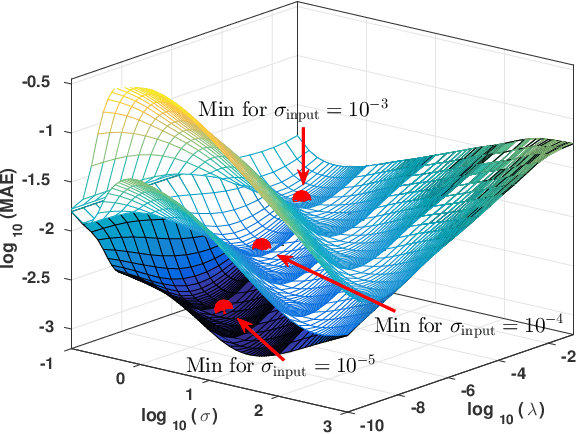
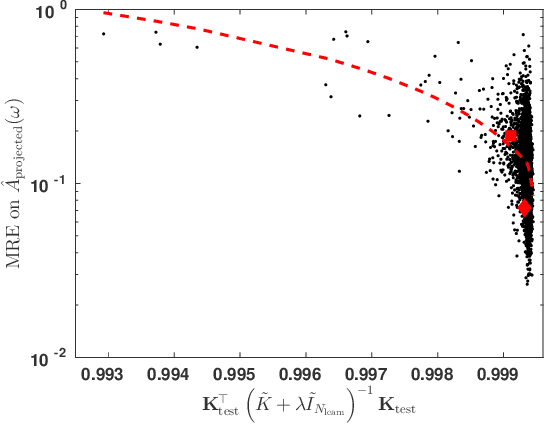
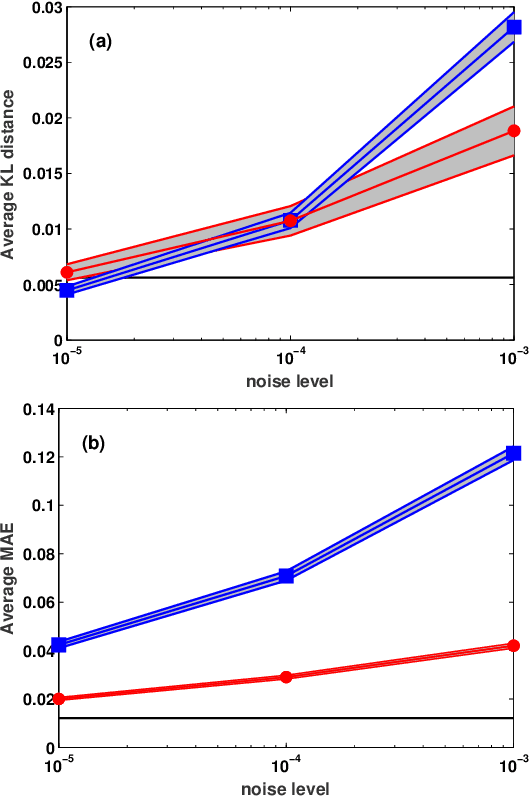
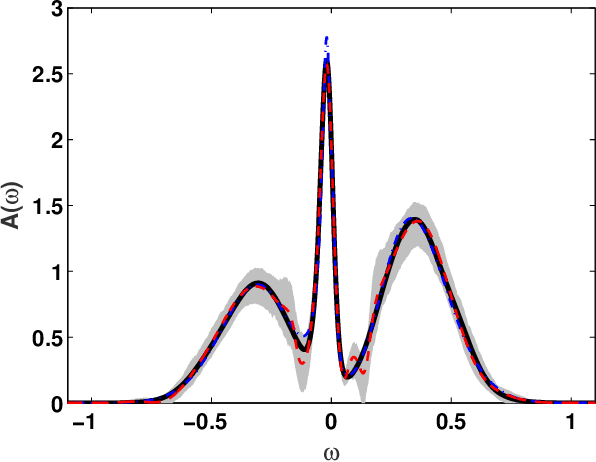
We present a machine learning approach to the inversion of Fredholm integrals of the first kind. The approach provides a natural regularization in cases where the inverse of the Fredholm kernel is ill-conditioned. It also provides an efficient and stable treatment of constraints. The key observation is that the stability of the forward problem permits the construction of a large database of outputs for physically meaningful inputs. We apply machine learning to this database to generate a regression function of controlled complexity, which returns approximate solutions for previously unseen inputs; the approximate solutions are then projected onto the subspace of functions satisfying relevant constraints. We also derive and present uncertainty estimates. We illustrate the approach by applying it to the analytical continuation problem of quantum many-body physics, which involves reconstructing the frequency dependence of physical excitation spectra from data obtained at specific points in the complex frequency plane. Under standard error metrics the method performs as well or better than the Maximum Entropy method for low input noise and is substantially more robust to increased input noise. We expect the methodology to be similarly effective for any problem involving a formally ill-conditioned inversion, provided that the forward problem can be efficiently solved.

Bayesian nonparametric multivariate convex regression

In many applications, such as economics, operations research and reinforcement learning, one often needs to estimate a multivariate regression function f subject to a convexity constraint. For example, in sequential decision processes the value of a state under optimal subsequent decisions may be known to be convex or concave. We propose a new Bayesian nonparametric multivariate approach based on characterizing the unknown regression function as the max of a random collection of unknown hyperplanes. This specification induces a prior with large support in a Kullback-Leibler sense on the space of convex functions, while also leading to strong posterior consistency. Although we assume that f is defined over R^p, we show that this model has a convergence rate of log(n)^{-1} n^{-1/(d+2)} under the empirical L2 norm when f actually maps a d dimensional linear subspace to R. We design an efficient reversible jump MCMC algorithm for posterior computation and demonstrate the methods through application to value function approximation.

Dirichlet Process Mixtures of Generalized Linear Models

We propose Dirichlet Process mixtures of Generalized Linear Models (DP-GLM), a new method of nonparametric regression that accommodates continuous and categorical inputs, and responses that can be modeled by a generalized linear model. We prove conditions for the asymptotic unbiasedness of the DP-GLM regression mean function estimate. We also give examples for when those conditions hold, including models for compactly supported continuous distributions and a model with continuous covariates and categorical response. We empirically analyze the properties of the DP-GLM and why it provides better results than existing Dirichlet process mixture regression models. We evaluate DP-GLM on several data sets, comparing it to modern methods of nonparametric regression like CART, Bayesian trees and Gaussian processes. Compared to existing techniques, the DP-GLM provides a single model (and corresponding inference algorithms) that performs well in many regression settings.

Stochastic Search with an Observable State Variable

In this paper we study convex stochastic search problems where a noisy objective function value is observed after a decision is made. There are many stochastic search problems whose behavior depends on an exogenous state variable which affects the shape of the objective function. Currently, there is no general purpose algorithm to solve this class of problems. We use nonparametric density estimation to take observations from the joint state-outcome distribution and use them to infer the optimal decision for a given query state. We propose two solution methods that depend on the problem characteristics: function-based and gradient-based optimization. We examine two weighting schemes, kernel-based weights and Dirichlet process-based weights, for use with the solution methods. The weights and solution methods are tested on a synthetic multi-product newsvendor problem and the hour-ahead wind commitment problem. Our results show that in some cases Dirichlet process weights offer substantial benefits over kernel based weights and more generally that nonparametric estimation methods provide good solutions to otherwise intractable problems.