Projected Regression Methods for Inverting Fredholm Integrals: Formalism and Application to Analytical Continuation
Paper and Code
Dec 15, 2016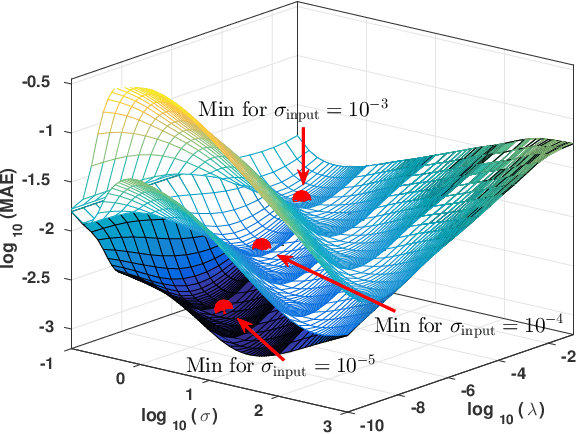
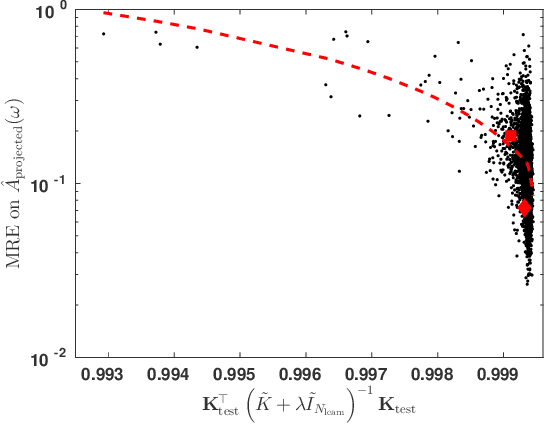
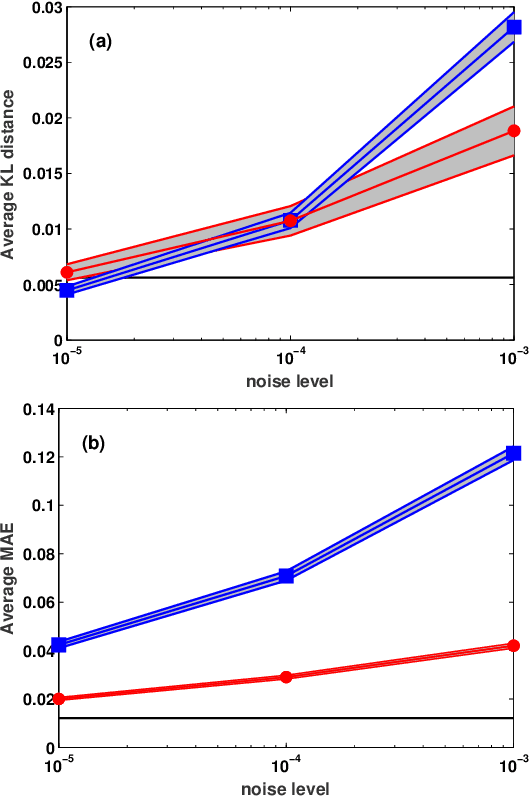
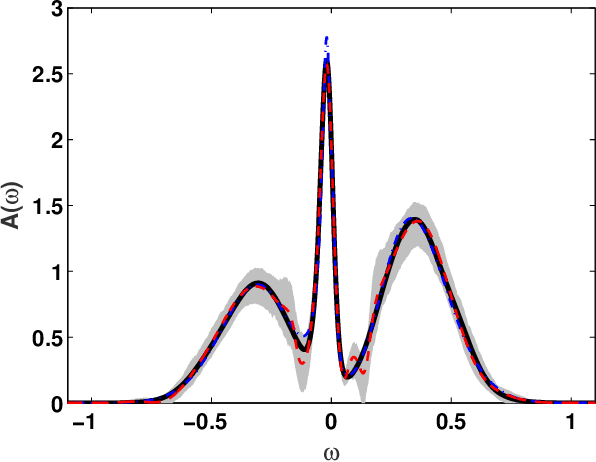
We present a machine learning approach to the inversion of Fredholm integrals of the first kind. The approach provides a natural regularization in cases where the inverse of the Fredholm kernel is ill-conditioned. It also provides an efficient and stable treatment of constraints. The key observation is that the stability of the forward problem permits the construction of a large database of outputs for physically meaningful inputs. We apply machine learning to this database to generate a regression function of controlled complexity, which returns approximate solutions for previously unseen inputs; the approximate solutions are then projected onto the subspace of functions satisfying relevant constraints. We also derive and present uncertainty estimates. We illustrate the approach by applying it to the analytical continuation problem of quantum many-body physics, which involves reconstructing the frequency dependence of physical excitation spectra from data obtained at specific points in the complex frequency plane. Under standard error metrics the method performs as well or better than the Maximum Entropy method for low input noise and is substantially more robust to increased input noise. We expect the methodology to be similarly effective for any problem involving a formally ill-conditioned inversion, provided that the forward problem can be efficiently solved.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge