Nonparametric Conditional Local Independence Testing

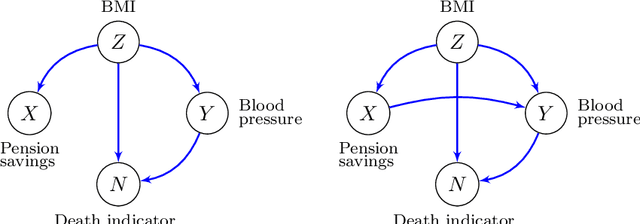
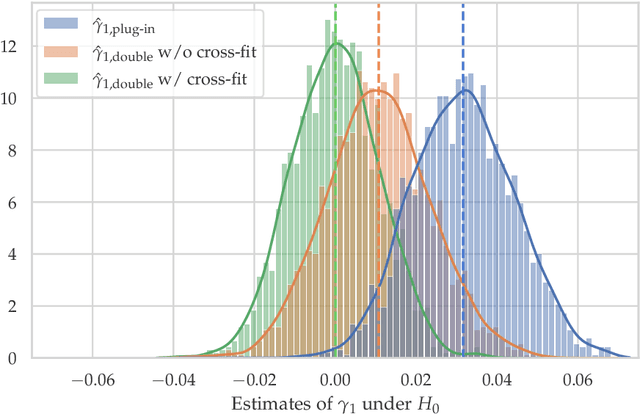
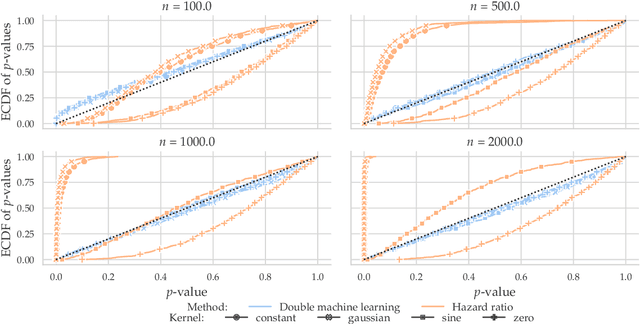
Conditional local independence is an independence relation among continuous time stochastic processes. It describes whether the evolution of one process is directly influenced by another process given the histories of additional processes, and it is important for the description and learning of causal relations among processes. However, no nonparametric test of conditional local independence has been available. We propose such a nonparametric test based on double machine learning. The test is based on a functional target parameter defined as the expectation of a stochastic integral. Under the hypothesis of conditional local independence the stochastic integral is a zero-mean martingale, and the target parameter is constantly equal to zero. We introduce the test statistic as an estimator of the target parameter and show that by using sample splitting or cross-fitting, its distributional limit is a Gaussian martingale under the hypothesis. Its variance function can be estimated consistently, and we derive specific univariate test statistics and their asymptotic distributions. An example based on a marginalized Cox model with time-dependent covariates is used throughout to illustrate the theory, and simulations based on this example show how double machine learning as well as sample splitting are needed for the test to work. Moreover, the simulation study shows that when both of these techniques are used in combination, the test works well without restrictive parametric assumptions.

Robustly Removing Deep Sea Lighting Effects for Visual Mapping of Abyssal Plains

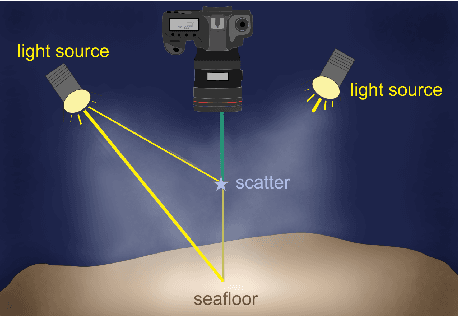
The majority of Earth's surface lies deep in the oceans, where no surface light reaches. Robots diving down to great depths must bring light sources that create moving illumination patterns in the darkness, such that the same 3D point appears with different color in each image. On top, scattering and attenuation of light in the water makes images appear foggy and typically blueish, the degradation depending on each pixel's distance to its observed seafloor patch, on the local composition of the water and the relative poses and cones of the light sources. Consequently, visual mapping, including image matching and surface albedo estimation, severely suffers from the effects that co-moving light sources produce, and larger mosaic maps from photos are often dominated by lighting effects that obscure the actual seafloor structure. In this contribution a practical approach to estimating and compensating these lighting effects on predominantly homogeneous, flat seafloor regions, as can be found in the Abyssal plains of our oceans, is presented. The method is essentially parameter-free and intended as a preprocessing step to facilitate visual mapping, but already produces convincing lighting artefact compensation up to a global white balance factor. It does not require to be trained beforehand on huge sets of annotated images, which are not available for the deep sea. Rather, we motivate our work by physical models of light propagation, perform robust statistics-based estimates of additive and multiplicative nuisances that avoid explicit parameters for light, camera, water or scene, discuss the breakdown point of the algorithms and show results on imagery captured by robots in several kilometer water depth.

Causal structure learning from time series: Large regression coefficients may predict causal links better in practice than small p-values

In this article, we describe the algorithms for causal structure learning from time series data that won the Causality 4 Climate competition at the Conference on Neural Information Processing Systems 2019 (NeurIPS). We examine how our combination of established ideas achieves competitive performance on semi-realistic and realistic time series data exhibiting common challenges in real-world Earth sciences data. In particular, we discuss a) a rationale for leveraging linear methods to identify causal links in non-linear systems, b) a simulation-backed explanation as to why large regression coefficients may predict causal links better in practice than small p-values and thus why normalising the data may sometimes hinder causal structure learning. For benchmark usage, we provide implementations at https://github.com/sweichwald/tidybench and detail the algorithms here. We propose the presented competition-proven methods for baseline benchmark comparisons to guide the development of novel algorithms for structure learning from time series.