Substitute adjustment via recovery of latent variables

The deconfounder was proposed as a method for estimating causal parameters in a context with multiple causes and unobserved confounding. It is based on recovery of a latent variable from the observed causes. We disentangle the causal interpretation from the statistical estimation problem and show that the deconfounder in general estimates adjusted regression target parameters. It does so by outcome regression adjusted for the recovered latent variable termed the substitute. We refer to the general algorithm, stripped of causal assumptions, as substitute adjustment. We give theoretical results to support that substitute adjustment estimates adjusted regression parameters when the regressors are conditionally independent given the latent variable. We also introduce a variant of our substitute adjustment algorithm that estimates an assumption-lean target parameter with minimal model assumptions. We then give finite sample bounds and asymptotic results supporting substitute adjustment estimation in the case where the latent variable takes values in a finite set. A simulation study illustrates finite sample properties of substitute adjustment. Our results support that when the latent variable model of the regressors hold, substitute adjustment is a viable method for adjusted regression.

Efficient adjustment for complex covariates: Gaining efficiency with DOPE

Covariate adjustment is a ubiquitous method used to estimate the average treatment effect (ATE) from observational data. Assuming a known graphical structure of the data generating model, recent results give graphical criteria for optimal adjustment, which enables efficient estimation of the ATE. However, graphical approaches are challenging for high-dimensional and complex data, and it is not straightforward to specify a meaningful graphical model of non-Euclidean data such as texts. We propose an general framework that accommodates adjustment for any subset of information expressed by the covariates. We generalize prior works and leverage these results to identify the optimal covariate information for efficient adjustment. This information is minimally sufficient for prediction of the outcome conditionally on treatment. Based on our theoretical results, we propose the Debiased Outcome-adapted Propensity Estimator (DOPE) for efficient estimation of the ATE, and we provide asymptotic results for the DOPE under general conditions. Compared to the augmented inverse propensity weighted (AIPW) estimator, the DOPE can retain its efficiency even when the covariates are highly predictive of treatment. We illustrate this with a single-index model, and with an implementation of the DOPE based on neural networks, we demonstrate its performance on simulated and real data. Our results show that the DOPE provides an efficient and robust methodology for ATE estimation in various observational settings.

Nonparametric Conditional Local Independence Testing

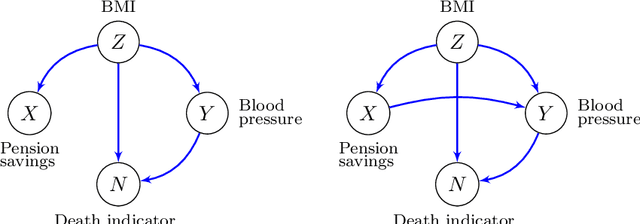
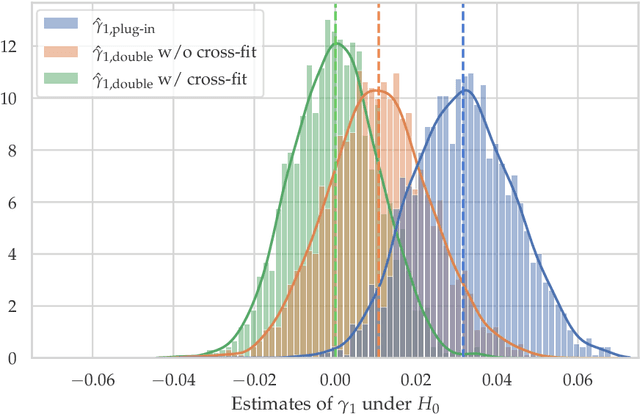
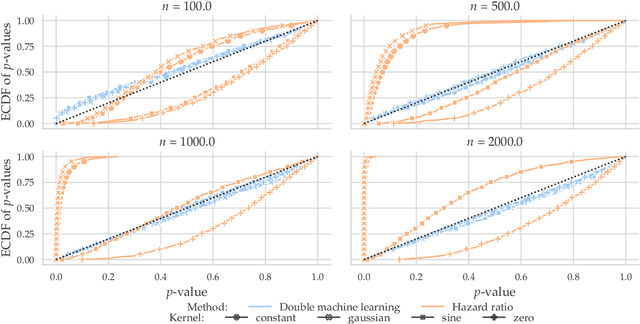
Conditional local independence is an independence relation among continuous time stochastic processes. It describes whether the evolution of one process is directly influenced by another process given the histories of additional processes, and it is important for the description and learning of causal relations among processes. However, no nonparametric test of conditional local independence has been available. We propose such a nonparametric test based on double machine learning. The test is based on a functional target parameter defined as the expectation of a stochastic integral. Under the hypothesis of conditional local independence the stochastic integral is a zero-mean martingale, and the target parameter is constantly equal to zero. We introduce the test statistic as an estimator of the target parameter and show that by using sample splitting or cross-fitting, its distributional limit is a Gaussian martingale under the hypothesis. Its variance function can be estimated consistently, and we derive specific univariate test statistics and their asymptotic distributions. An example based on a marginalized Cox model with time-dependent covariates is used throughout to illustrate the theory, and simulations based on this example show how double machine learning as well as sample splitting are needed for the test to work. Moreover, the simulation study shows that when both of these techniques are used in combination, the test works well without restrictive parametric assumptions.

Local Independence Testing for Point Processes

Constraint based causal structure learning for point processes require empirical tests of local independence. Existing tests require strong model assumptions, e.g. that the true data generating model is a Hawkes process with no latent confounders. Even when restricting attention to Hawkes processes, latent confounders are a major technical difficulty because a marginalized process will generally not be a Hawkes process itself. We introduce an expansion similar to Volterra expansions as a tool to represent marginalized intensities. Our main theoretical result is that such expansions can approximate the true marginalized intensity arbitrarily well. Based on this we propose a test of local independence and investigate its properties in real and simulated data.

Graphical continuous Lyapunov models

The linear Lyapunov equation of a covariance matrix parametrizes the equilibrium covariance matrix of a stochastic process. This parametrization can be interpreted as a new graphical model class, and we show how the model class behaves under marginalization and introduce a method for structure learning via $\ell_1$-penalized loss minimization. Our proposed method is demonstrated to outperform alternative structure learning algorithms in a simulation study, and we illustrate its application for protein phosphorylation network reconstruction.

Penalized estimation in large-scale generalized linear array models

Large-scale generalized linear array models (GLAMs) can be challenging to fit. Computation and storage of its tensor product design matrix can be impossible due to time and memory constraints, and previously considered design matrix free algorithms do not scale well with the dimension of the parameter vector. A new design matrix free algorithm is proposed for computing the penalized maximum likelihood estimate for GLAMs, which, in particular, handles nondifferentiable penalty functions. The proposed algorithm is implemented and available via the R package \verb+glamlasso+. It combines several ideas -- previously considered separately -- to obtain sparse estimates while at the same time efficiently exploiting the GLAM structure. In this paper the convergence of the algorithm is treated and the performance of its implementation is investigated and compared to that of \verb+glmnet+ on simulated as well as real data. It is shown that the computation time for

Sparse group lasso and high dimensional multinomial classification

The sparse group lasso optimization problem is solved using a coordinate gradient descent algorithm. The algorithm is applicable to a broad class of convex loss functions. Convergence of the algorithm is established, and the algorithm is used to investigate the performance of the multinomial sparse group lasso classifier. On three different real data examples the multinomial group lasso clearly outperforms multinomial lasso in terms of achieved classification error rate and in terms of including fewer features for the classification. The run-time of our sparse group lasso implementation is of the same order of magnitude as the multinomial lasso algorithm implemented in the R package glmnet. Our implementation scales well with the problem size. One of the high dimensional examples considered is a 50 class classification problem with 10k features, which amounts to estimating 500k parameters. The implementation is available as the R package msgl.