Model-free Methods for Event History Analysis and Efficient Adjustment (PhD Thesis)

This thesis contains a series of independent contributions to statistics, unified by a model-free perspective. The first chapter elaborates on how a model-free perspective can be used to formulate flexible methods that leverage prediction techniques from machine learning. Mathematical insights are obtained from concrete examples, and these insights are generalized to principles that permeate the rest of the thesis. The second chapter studies the concept of local independence, which describes whether the evolution of one stochastic process is directly influenced by another. To test local independence, we define a model-free parameter called the Local Covariance Measure (LCM). We formulate an estimator for the LCM, from which a test of local independence is proposed. We discuss how the size and power of the proposed test can be controlled uniformly and investigate the test in a simulation study. The third chapter focuses on covariate adjustment, a method used to estimate the effect of a treatment by accounting for observed confounding. We formulate a general framework that facilitates adjustment for any subset of covariate information. We identify the optimal covariate information for adjustment and, based on this, introduce the Debiased Outcome-adapted Propensity Estimator (DOPE) for efficient estimation of treatment effects. An instance of DOPE is implemented using neural networks, and we demonstrate its performance on simulated and real data. The fourth and final chapter introduces a model-free measure of the conditional association between an exposure and a time-to-event, which we call the Aalen Covariance Measure (ACM). We develop a model-free estimation method and show that it is doubly robust, ensuring $\sqrt{n}$-consistency provided that the nuisance functions can be estimated with modest rates. A simulation study demonstrates the use of our estimator in several settings.

Efficient adjustment for complex covariates: Gaining efficiency with DOPE

Covariate adjustment is a ubiquitous method used to estimate the average treatment effect (ATE) from observational data. Assuming a known graphical structure of the data generating model, recent results give graphical criteria for optimal adjustment, which enables efficient estimation of the ATE. However, graphical approaches are challenging for high-dimensional and complex data, and it is not straightforward to specify a meaningful graphical model of non-Euclidean data such as texts. We propose an general framework that accommodates adjustment for any subset of information expressed by the covariates. We generalize prior works and leverage these results to identify the optimal covariate information for efficient adjustment. This information is minimally sufficient for prediction of the outcome conditionally on treatment. Based on our theoretical results, we propose the Debiased Outcome-adapted Propensity Estimator (DOPE) for efficient estimation of the ATE, and we provide asymptotic results for the DOPE under general conditions. Compared to the augmented inverse propensity weighted (AIPW) estimator, the DOPE can retain its efficiency even when the covariates are highly predictive of treatment. We illustrate this with a single-index model, and with an implementation of the DOPE based on neural networks, we demonstrate its performance on simulated and real data. Our results show that the DOPE provides an efficient and robust methodology for ATE estimation in various observational settings.

Nonparametric Conditional Local Independence Testing

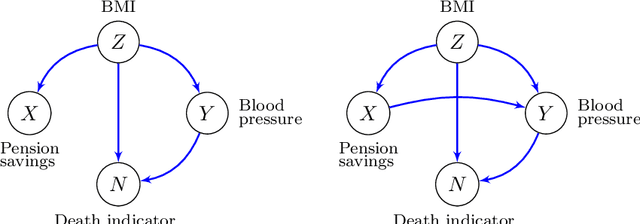
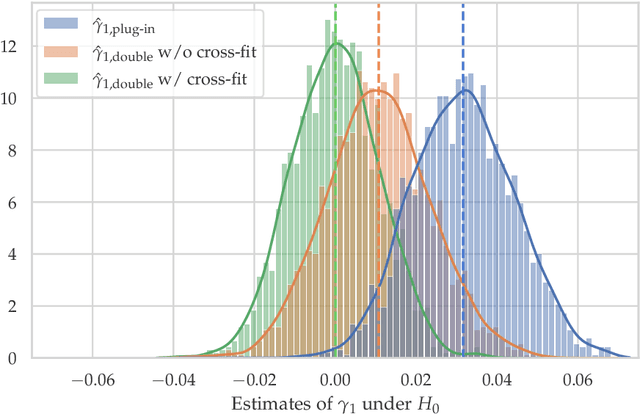
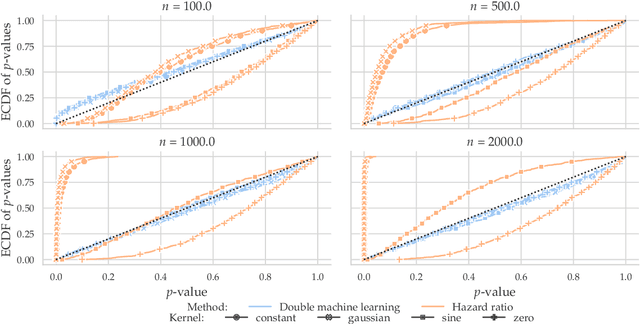
Conditional local independence is an independence relation among continuous time stochastic processes. It describes whether the evolution of one process is directly influenced by another process given the histories of additional processes, and it is important for the description and learning of causal relations among processes. However, no nonparametric test of conditional local independence has been available. We propose such a nonparametric test based on double machine learning. The test is based on a functional target parameter defined as the expectation of a stochastic integral. Under the hypothesis of conditional local independence the stochastic integral is a zero-mean martingale, and the target parameter is constantly equal to zero. We introduce the test statistic as an estimator of the target parameter and show that by using sample splitting or cross-fitting, its distributional limit is a Gaussian martingale under the hypothesis. Its variance function can be estimated consistently, and we derive specific univariate test statistics and their asymptotic distributions. An example based on a marginalized Cox model with time-dependent covariates is used throughout to illustrate the theory, and simulations based on this example show how double machine learning as well as sample splitting are needed for the test to work. Moreover, the simulation study shows that when both of these techniques are used in combination, the test works well without restrictive parametric assumptions.