Explicit and data-Efficient Encoding via Gradient Flow

The autoencoder model typically uses an encoder to map data to a lower dimensional latent space and a decoder to reconstruct it. However, relying on an encoder for inversion can lead to suboptimal representations, particularly limiting in physical sciences where precision is key. We introduce a decoder-only method using gradient flow to directly encode data into the latent space, defined by ordinary differential equations (ODEs). This approach eliminates the need for approximate encoder inversion. We train the decoder via the adjoint method and show that costly integrals can be avoided with minimal accuracy loss. Additionally, we propose a $2^{nd}$ order ODE variant, approximating Nesterov's accelerated gradient descent for faster convergence. To handle stiff ODEs, we use an adaptive solver that prioritizes loss minimization, improving robustness. Compared to traditional autoencoders, our method demonstrates explicit encoding and superior data efficiency, which is crucial for data-scarce scenarios in the physical sciences. Furthermore, this work paves the way for integrating machine learning into scientific workflows, where precise and efficient encoding is critical. \footnote{The code for this work is available at \url{https://github.com/k-flouris/gfe}.}

Energy-Based Prior Latent Space Diffusion model for Reconstruction of Lumbar Vertebrae from Thick Slice MRI

Lumbar spine problems are ubiquitous, motivating research into targeted imaging for treatment planning and guided interventions. While high resolution and high contrast CT has been the modality of choice, MRI can capture both bone and soft tissue without the ionizing radiation of CT albeit longer acquisition time. The critical trade-off between contrast quality and acquisition time has motivated 'thick slice MRI', which prioritises faster imaging with high in-plane resolution but variable contrast and low through-plane resolution. We investigate a recently developed post-acquisition pipeline which segments vertebrae from thick-slice acquisitions and uses a variational autoencoder to enhance quality after an initial 3D reconstruction. We instead propose a latent space diffusion energy-based prior to leverage diffusion models, which exhibit high-quality image generation. Crucially, we mitigate their high computational cost and low sample efficiency by learning an energy-based latent representation to perform the diffusion processes. Our resulting method outperforms existing approaches across metrics including Dice and VS scores, and more faithfully captures 3D features.

A Matrix Product State Model for Simultaneous Classification and Generation

Quantum machine learning (QML) is a rapidly expanding field that merges the principles of quantum computing with the techniques of machine learning. One of the powerful mathematical frameworks in this domain is tensor networks. These networks are used to approximate high-order tensors by contracting tensors with lower ranks. Originally developed for simulating quantum systems, tensor networks have become integral to quantum computing and, by extension, to QML. Their ability to efficiently represent and manipulate complex, high-dimensional data makes them suitable for various machine learning tasks within the quantum realm. Here, we present a matrix product state (MPS) model, where the MPS functions as both a classifier and a generator. The dual functionality of this novel MPS model permits a strategy that enhances the traditional training of supervised MPS models. This framework is inspired by generative adversarial networks and is geared towards generating more realistic samples by reducing outliers. Additionally, our contributions offer insights into the mechanics of tensor network methods for generation tasks. Specifically, we discuss alternative embedding functions and a new sampling method from non-normalized MPSs.

Canonical normalizing flows for manifold learning

Manifold learning flows are a class of generative modelling techniques that assume a low-dimensional manifold description of the data. The embedding of such a manifold into the high-dimensional space of the data is achieved via learnable invertible transformations. Therefore, once the manifold is properly aligned via a reconstruction loss, the probability density is tractable on the manifold and maximum likelihood can be used to optimize the network parameters. Naturally, the lower-dimensional representation of the data requires an injective-mapping. Recent approaches were able to enforce that the density aligns with the modelled manifold, while efficiently calculating the density volume-change term when embedding to the higher-dimensional space. However, unless the injective-mapping is analytically predefined, the learned manifold is not necessarily an efficient representation of the data. Namely, the latent dimensions of such models frequently learn an entangled intrinsic basis, with degenerate information being stored in each dimension. Alternatively, if a locally orthogonal and/or sparse basis is to be learned, here coined canonical intrinsic basis, it can serve in learning a more compact latent space representation. Toward this end, we propose a canonical manifold learning flow method, where a novel optimization objective enforces the transformation matrix to have few prominent and non-degenerate basis functions. We demonstrate that by minimizing the off-diagonal manifold metric elements $\ell_1$-norm, we can achieve such a basis, which is simultaneously sparse and/or orthogonal. Canonical manifold flow yields a more efficient use of the latent space, automatically generating fewer prominent and distinct dimensions to represent data, and a better approximation of target distributions than other manifold flow methods in most experiments we conducted, resulting in lower FID scores.

Explicitly Minimizing the Blur Error of Variational Autoencoders

Variational autoencoders (VAEs) are powerful generative modelling methods, however they suffer from blurry generated samples and reconstructions compared to the images they have been trained on. Significant research effort has been spent to increase the generative capabilities by creating more flexible models but often flexibility comes at the cost of higher complexity and computational cost. Several works have focused on altering the reconstruction term of the evidence lower bound (ELBO), however, often at the expense of losing the mathematical link to maximizing the likelihood of the samples under the modeled distribution. Here we propose a new formulation of the reconstruction term for the VAE that specifically penalizes the generation of blurry images while at the same time still maximizing the ELBO under the modeled distribution. We show the potential of the proposed loss on three different data sets, where it outperforms several recently proposed reconstruction losses for VAEs.

Gradient flow encoding with distance optimization adaptive step size

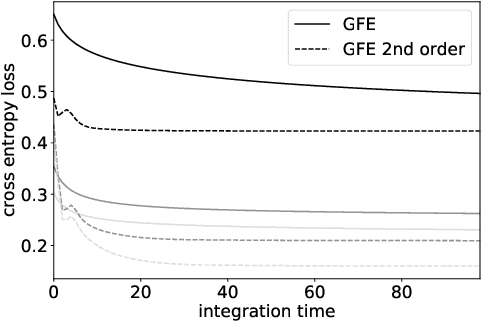
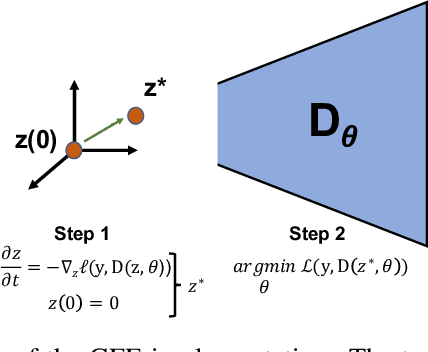
The autoencoder model uses an encoder to map data samples to a lower dimensional latent space and then a decoder to map the latent space representations back to the data space. Implicitly, it relies on the encoder to approximate the inverse of the decoder network, so that samples can be mapped to and back from the latent space faithfully. This approximation may lead to sub-optimal latent space representations. In this work, we investigate a decoder-only method that uses gradient flow to encode data samples in the latent space. The gradient flow is defined based on a given decoder and aims to find the optimal latent space representation for any given sample through optimisation, eliminating the need of an approximate inversion through an encoder. Implementing gradient flow through ordinary differential equations (ODE), we leverage the adjoint method to train a given decoder. We further show empirically that the costly integrals in the adjoint method may not be entirely necessary. Additionally, we propose a $2^{nd}$ order ODE variant to the method, which approximates Nesterov's accelerated gradient descent, with faster convergence per iteration. Commonly used ODE solvers can be quite sensitive to the integration step-size depending on the stiffness of the ODE. To overcome the sensitivity for gradient flow encoding, we use an adaptive solver that prioritises minimising loss at each integration step. We assess the proposed method in comparison to the autoencoding model. In our experiments, GFE showed a much higher data-efficiency than the autoencoding model, which can be crucial for data scarce applications.