Compressive Sensing of ECG Signals using Plug-and-Play Regularization

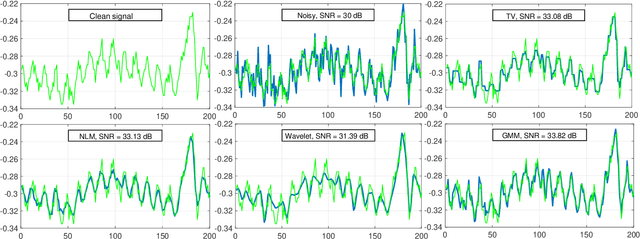
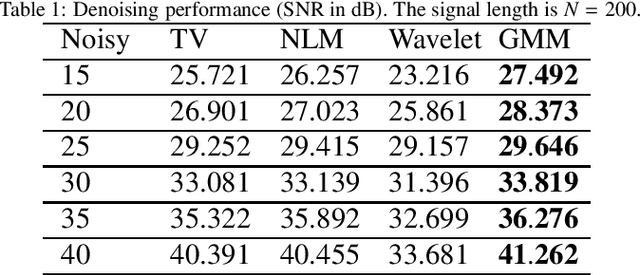
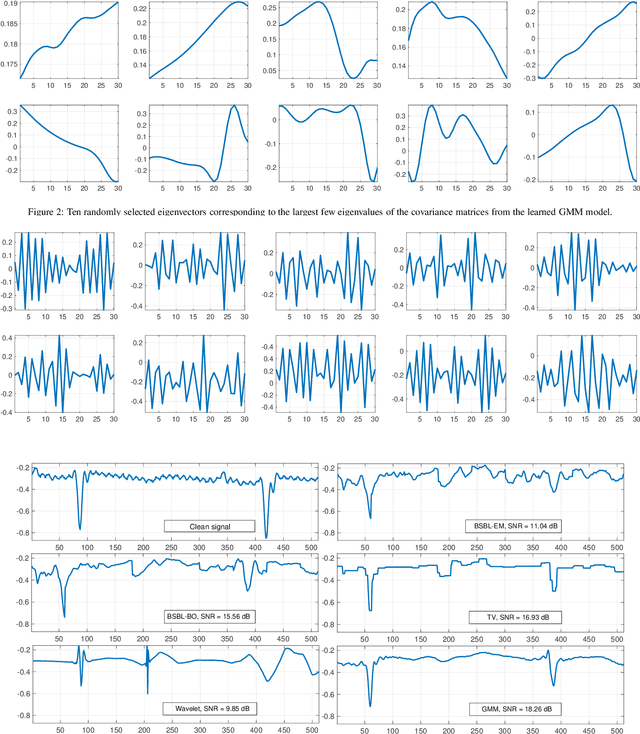
Compressive Sensing (CS) has recently attracted attention for ECG data compression. In CS, an ECG signal is projected onto a small set of random vectors. Recovering the original signal from such compressed measurements remains a challenging problem. Traditional recovery methods are based on solving a regularized minimization problem, where a sparsity-promoting prior is used. In this paper, we propose an alternative iterative recovery algorithm based on the Plug-and-Play (PnP) method, which has recently become popular for imaging problems. In PnP, a powerful denoiser is used to implicitly perform regularization, instead of using hand-crafted regularizers; this has been found to be more successful than traditional methods. In this work, we use a PnP version of the Proximal Gradient Descent (PGD) algorithm for ECG recovery. To ensure mathematical convergence of the PnP algorithm, the signal denoiser in question needs to satisfy some technical conditions. We use a high-quality ECG signal denoiser fulfilling this condition by learning a Bayesian prior for small-sized signal patches. This guarantees that the proposed algorithm converges to a fixed point irrespective of the initialization. Importantly, through extensive experiments, we show that the reconstruction quality of the proposed method is superior to that of state-of-the-art methods.

Least-squares registration of point sets over SE using closed-form projections

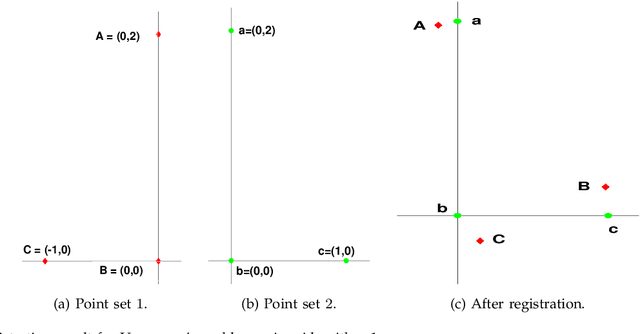
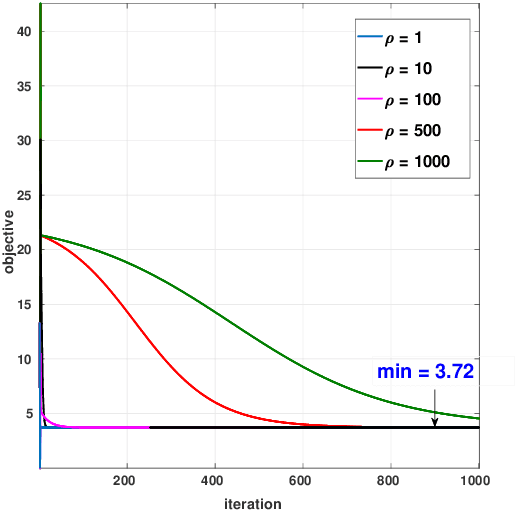
Consider the problem of registering multiple point sets in some $d$-dimensional space using rotations and translations. Assume that there are sets with common points, and moreover the pairwise correspondences are known for such sets. We consider a least-squares formulation of this problem, where the variables are the transforms associated with the point sets. The present novelty is that we reduce this nonconvex problem to an optimization over the positive semidefinite cone, where the objective is linear but the constraints are nevertheless nonconvex. We propose to solve this using variable splitting and the alternating directions method of multipliers (ADMM). Due to the linearity of the objective and the structure of constraints, the ADMM subproblems are given by projections with closed-form solutions. In particular, for $m$ point sets, the dominant cost per iteration is the partial eigendecomposition of an $md \times md$ matrix, and $m-1$ singular value decompositions of $d \times d$ matrices. We empirically show that for appropriate parameter settings, the proposed solver has a large convergence basin and is stable under perturbations. As applications, we use our method for $2$D shape matching and $3$D multiview registration. In either application, we model the shapes/scans as point sets and determine the pairwise correspondences using ICP. In particular, our algorithm compares favorably with existing methods for multiview reconstruction in terms of timing and accuracy.

A Simple Yet Effective Improvement to the Bilateral Filter for Image Denoising

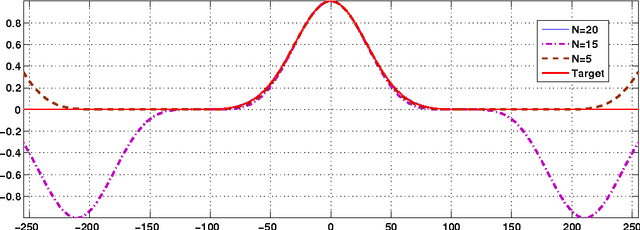
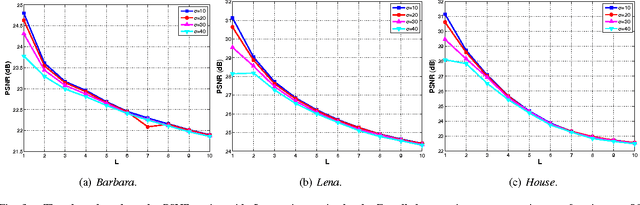
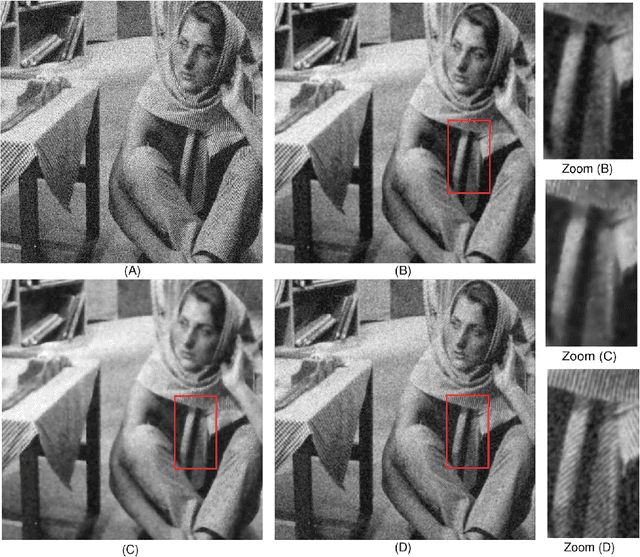
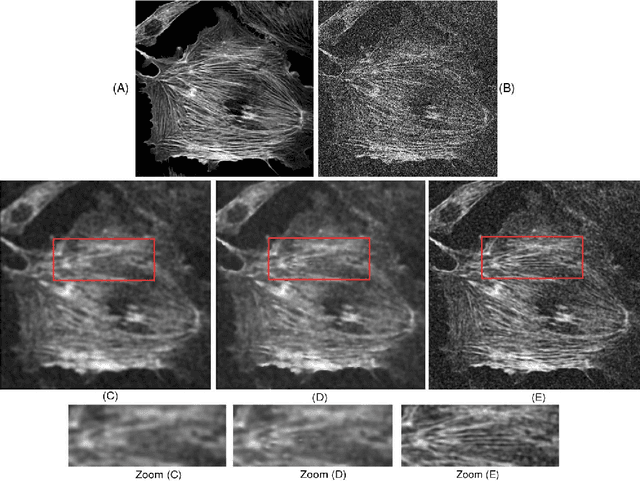
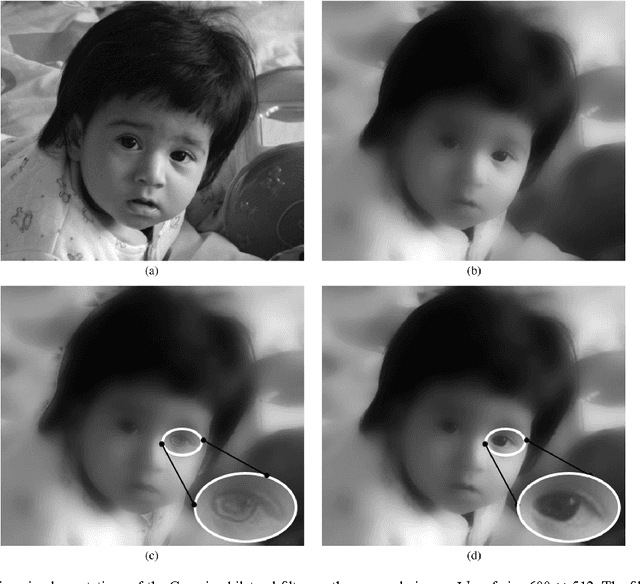
The bilateral filter has diverse applications in image processing, computer vision, and computational photography. In particular, this non-linear filter is quite effective in denoising images corrupted with additive Gaussian noise. The filter, however, is known to perform poorly at large noise levels. Several adaptations of the filter have been proposed in the literature to address this shortcoming, but often at an added computational cost. In this paper, we report a simple yet effective modification that improves the denoising performance of the bilateral filter at almost no additional cost. We provide visual and quantitative results on standard test images which show that this improvement is significant both visually and in terms of PSNR and SSIM (often as large as 5 dB). We also demonstrate how the proposed filtering can be implemented at reduced complexity by adapting a recent idea for fast bilateral filtering.

A radial version of the Central Limit Theorem

In this note, we give a probabilistic interpretation of the Central Limit Theorem used for approximating isotropic Gaussians in [1].

Fast space-variant elliptical filtering using box splines

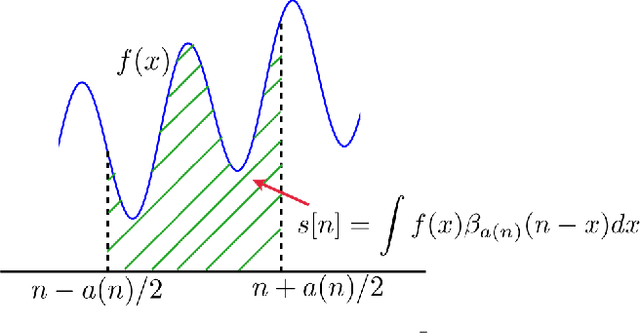
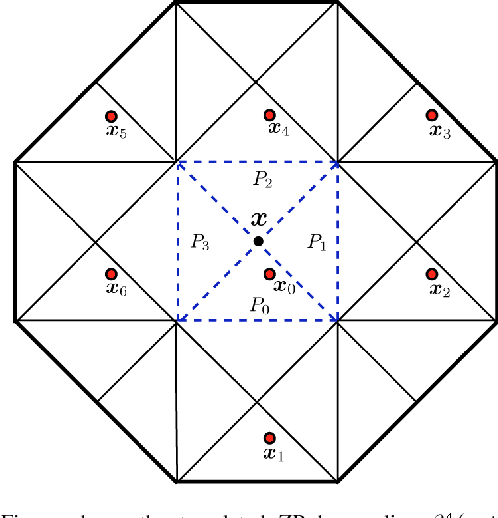
The efficient realization of linear space-variant (non-convolution) filters is a challenging computational problem in image processing. In this paper, we demonstrate that it is possible to filter an image with a Gaussian-like elliptic window of varying size, elongation and orientation using a fixed number of computations per pixel. The associated algorithm, which is based on a family of smooth compactly supported piecewise polynomials, the radially-uniform box splines, is realized using pre-integration and local finite-differences. The radially-uniform box splines are constructed through the repeated convolution of a fixed number of box distributions, which have been suitably scaled and distributed radially in an uniform fashion. The attractive features of these box splines are their asymptotic behavior, their simple covariance structure, and their quasi-separability. They converge to Gaussians with the increase of their order, and are used to approximate anisotropic Gaussians of varying covariance simply by controlling the scales of the constituent box distributions. Based on the second feature, we develop a technique for continuously controlling the size, elongation and orientation of these Gaussian-like functions. Finally, the quasi-separable structure, along with a certain scaling property of box distributions, is used to efficiently realize the associated space-variant elliptical filtering, which requires O(1) computations per pixel irrespective of the shape and size of the filter.

Constant-time filtering using shiftable kernels

It was recently demonstrated in [5] that the non-linear bilateral filter [14] can be efficiently implemented using a constant-time or O(1) algorithm. At the heart of this algorithm was the idea of approximating the Gaussian range kernel of the bilateral filter using trigonometric functions. In this letter, we explain how the idea in [5] can be extended to few other linear and non-linear filters [14, 17, 2]. While some of these filters have received a lot of attention in recent years, they are known to be computationally intensive. To extend the idea in [5], we identify a central property of trigonometric functions, called shiftability, that allows us to exploit the redundancy inherent in the filtering operations. In particular, using shiftable kernels, we show how certain complex filtering can be reduced to simply that of computing the moving sum of a stack of images. Each image in the stack is obtained through an elementary pointwise transform of the input image. This has a two-fold advantage. First, we can use fast recursive algorithms for computing the moving sum [15, 6], and, secondly, we can use parallel computation to further speed up the computation. We also show how shiftable kernels can also be used to approximate the (non-shiftable) Gaussian kernel that is ubiquitously used in image filtering.

Fast O(1) bilateral filtering using trigonometric range kernels

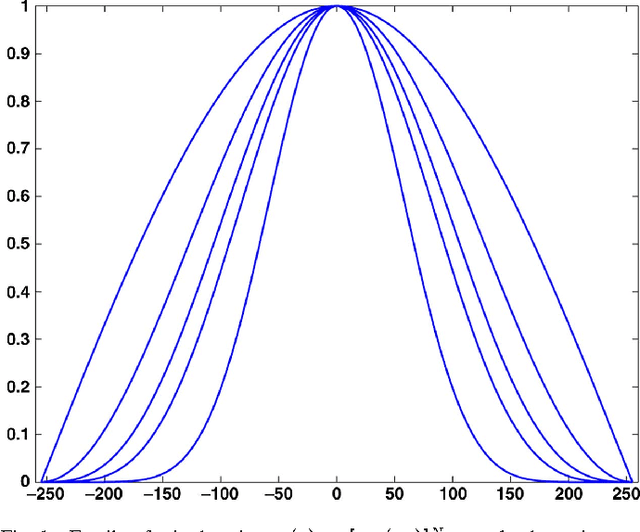
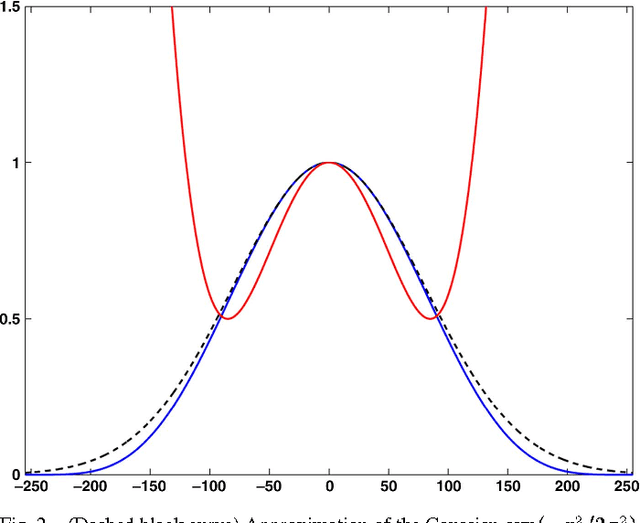
It is well-known that spatial averaging can be realized (in space or frequency domain) using algorithms whose complexity does not depend on the size or shape of the filter. These fast algorithms are generally referred to as constant-time or O(1) algorithms in the image processing literature. Along with the spatial filter, the edge-preserving bilateral filter [Tomasi1998] involves an additional range kernel. This is used to restrict the averaging to those neighborhood pixels whose intensity are similar or close to that of the pixel of interest. The range kernel operates by acting on the pixel intensities. This makes the averaging process non-linear and computationally intensive, especially when the spatial filter is large. In this paper, we show how the O(1) averaging algorithms can be leveraged for realizing the bilateral filter in constant-time, by using trigonometric range kernels. This is done by generalizing the idea in [Porikli2008] of using polynomial range kernels. The class of trigonometric kernels turns out to be sufficiently rich, allowing for the approximation of the standard Gaussian bilateral filter. The attractive feature of our approach is that, for a fixed number of terms, the quality of approximation achieved using trigonometric kernels is much superior to that obtained in [Porikli2008] using polynomials.

On the Hilbert transform of wavelets

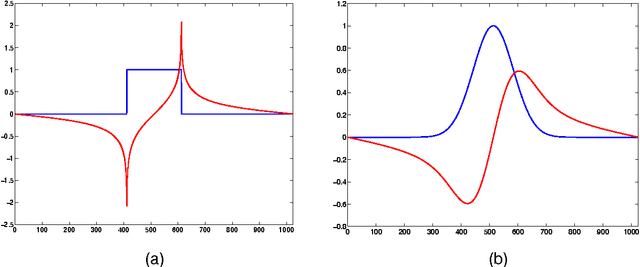
A wavelet is a localized function having a prescribed number of vanishing moments. In this correspondence, we provide precise arguments as to why the Hilbert transform of a wavelet is again a wavelet. In particular, we provide sharp estimates of the localization, vanishing moments, and smoothness of the transformed wavelet. We work in the general setting of non-compactly supported wavelets. Our main result is that, in the presence of some minimal smoothness and decay, the Hilbert transform of a wavelet is again as smooth and oscillating as the original wavelet, whereas its localization is controlled by the number of vanishing moments of the original wavelet. We motivate our results using concrete examples.

Fast adaptive elliptical filtering using box splines

We demonstrate that it is possible to filter an image with an elliptic window of varying size, elongation and orientation with a fixed computational cost per pixel. Our method involves the application of a suitable global pre-integrator followed by a pointwise-adaptive localization mesh. We present the basic theory for the 1D case using a B-spline formalism and then appropriately extend it to 2D using radially-uniform box splines. The size and ellipticity of these radially-uniform box splines is adaptively controlled. Moreover, they converge to Gaussians as the order increases. Finally, we present a fast and practical directional filtering algorithm that has the capability of adapting to the local image features.

Gabor wavelet analysis and the fractional Hilbert transform

We propose an amplitude-phase representation of the dual-tree complex wavelet transform (DT-CWT) which provides an intuitive interpretation of the associated complex wavelet coefficients. The representation, in particular, is based on the shifting action of the group of fractional Hilbert transforms (fHT) which allow us to extend the notion of arbitrary phase-shifts beyond pure sinusoids. We explicitly characterize this shifting action for a particular family of Gabor-like wavelets which, in effect, links the corresponding dual-tree transform with the framework of windowed-Fourier analysis. We then extend these ideas to the bivariate DT-CWT based on certain directional extensions of the fHT. In particular, we derive a signal representation involving the superposition of direction-selective wavelets affected with appropriate phase-shifts.