Least-squares registration of point sets over SE using closed-form projections
Paper and Code
Apr 12, 2019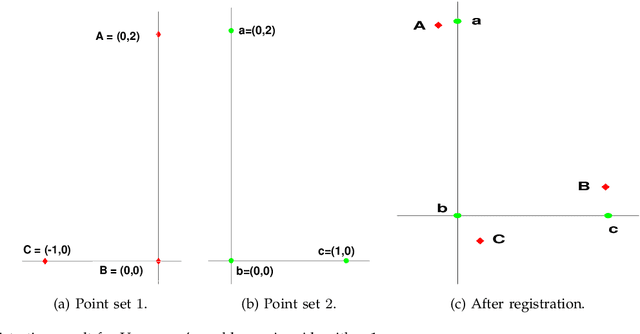


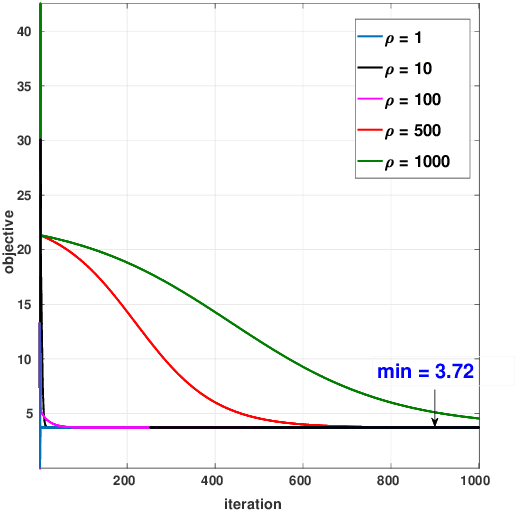
Consider the problem of registering multiple point sets in some $d$-dimensional space using rotations and translations. Assume that there are sets with common points, and moreover the pairwise correspondences are known for such sets. We consider a least-squares formulation of this problem, where the variables are the transforms associated with the point sets. The present novelty is that we reduce this nonconvex problem to an optimization over the positive semidefinite cone, where the objective is linear but the constraints are nevertheless nonconvex. We propose to solve this using variable splitting and the alternating directions method of multipliers (ADMM). Due to the linearity of the objective and the structure of constraints, the ADMM subproblems are given by projections with closed-form solutions. In particular, for $m$ point sets, the dominant cost per iteration is the partial eigendecomposition of an $md \times md$ matrix, and $m-1$ singular value decompositions of $d \times d$ matrices. We empirically show that for appropriate parameter settings, the proposed solver has a large convergence basin and is stable under perturbations. As applications, we use our method for $2$D shape matching and $3$D multiview registration. In either application, we model the shapes/scans as point sets and determine the pairwise correspondences using ICP. In particular, our algorithm compares favorably with existing methods for multiview reconstruction in terms of timing and accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge