JDLL: A library to run Deep Learning models on Java bioimage informatics platforms

We present JDLL, an agile Java library that offers a comprehensive toolset/API to unify the development of high-end applications of DL for bioimage analysis and to streamline their installation and maintenance. JDLL provides all the functions required to consume DL models seamlessly, without being burdened by the configuration of the Python-based DL frameworks, within Java bioimage informatics platforms. Moreover, it allows the deployment of pre-trained models in the Bioimage Model Zoo (BMZ) by shipping the logic to connect to the BMZ website, download and run a selected model inference.

Fast space-variant elliptical filtering using box splines

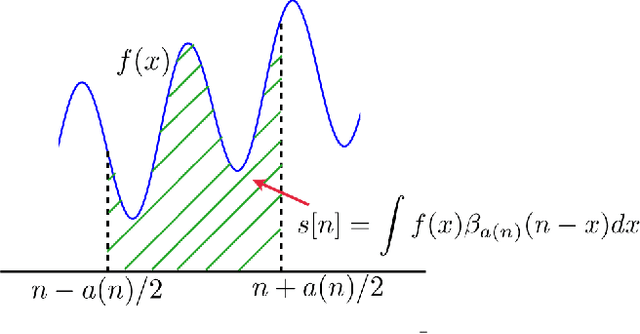
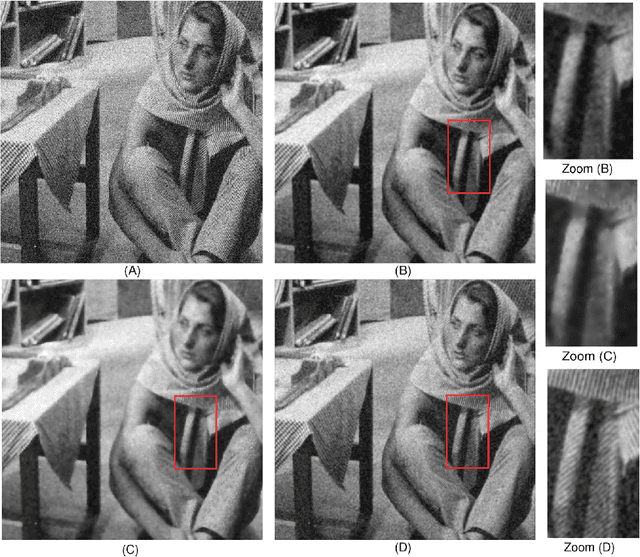
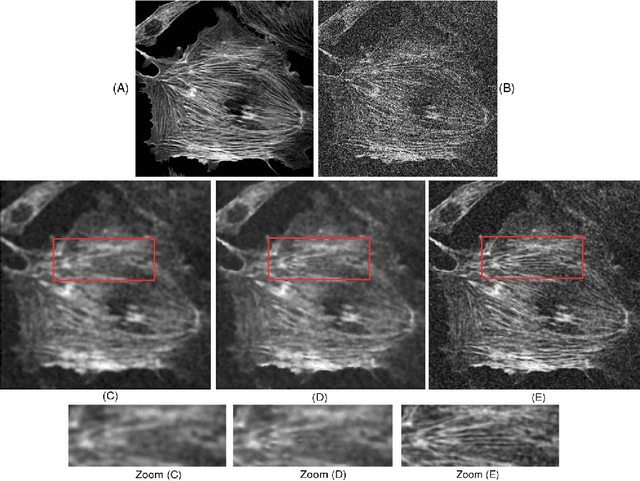
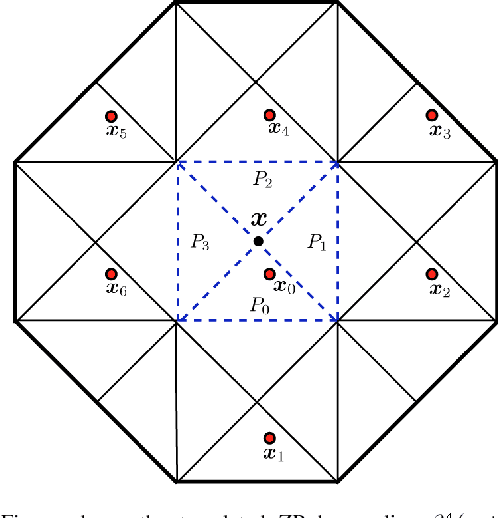
The efficient realization of linear space-variant (non-convolution) filters is a challenging computational problem in image processing. In this paper, we demonstrate that it is possible to filter an image with a Gaussian-like elliptic window of varying size, elongation and orientation using a fixed number of computations per pixel. The associated algorithm, which is based on a family of smooth compactly supported piecewise polynomials, the radially-uniform box splines, is realized using pre-integration and local finite-differences. The radially-uniform box splines are constructed through the repeated convolution of a fixed number of box distributions, which have been suitably scaled and distributed radially in an uniform fashion. The attractive features of these box splines are their asymptotic behavior, their simple covariance structure, and their quasi-separability. They converge to Gaussians with the increase of their order, and are used to approximate anisotropic Gaussians of varying covariance simply by controlling the scales of the constituent box distributions. Based on the second feature, we develop a technique for continuously controlling the size, elongation and orientation of these Gaussian-like functions. Finally, the quasi-separable structure, along with a certain scaling property of box distributions, is used to efficiently realize the associated space-variant elliptical filtering, which requires O(1) computations per pixel irrespective of the shape and size of the filter.