Compressive Sensing of ECG Signals using Plug-and-Play Regularization
Paper and Code
Oct 15, 2022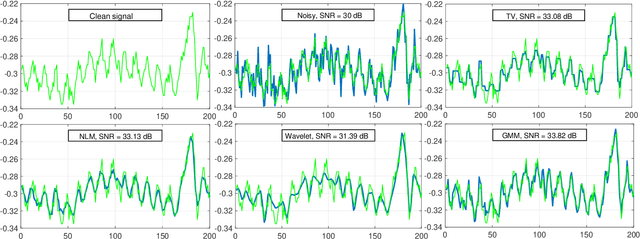
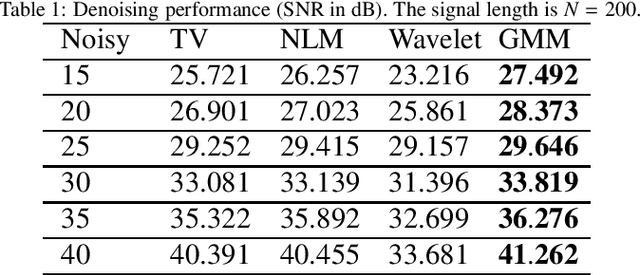

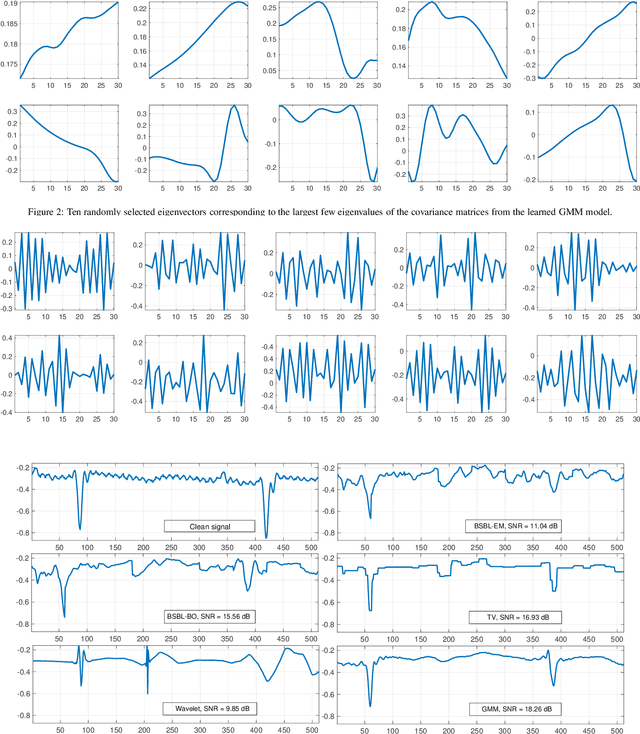
Compressive Sensing (CS) has recently attracted attention for ECG data compression. In CS, an ECG signal is projected onto a small set of random vectors. Recovering the original signal from such compressed measurements remains a challenging problem. Traditional recovery methods are based on solving a regularized minimization problem, where a sparsity-promoting prior is used. In this paper, we propose an alternative iterative recovery algorithm based on the Plug-and-Play (PnP) method, which has recently become popular for imaging problems. In PnP, a powerful denoiser is used to implicitly perform regularization, instead of using hand-crafted regularizers; this has been found to be more successful than traditional methods. In this work, we use a PnP version of the Proximal Gradient Descent (PGD) algorithm for ECG recovery. To ensure mathematical convergence of the PnP algorithm, the signal denoiser in question needs to satisfy some technical conditions. We use a high-quality ECG signal denoiser fulfilling this condition by learning a Bayesian prior for small-sized signal patches. This guarantees that the proposed algorithm converges to a fixed point irrespective of the initialization. Importantly, through extensive experiments, we show that the reconstruction quality of the proposed method is superior to that of state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge