Implicit Variational Inference for High-Dimensional Posteriors

In variational inference, the benefits of Bayesian models rely on accurately capturing the true posterior distribution. We propose using neural samplers that specify implicit distributions, which are well-suited for approximating complex multimodal and correlated posteriors in high-dimensional spaces. Our approach advances inference using implicit distributions by introducing novel bounds that come about by locally linearising the neural sampler. This is distinct from existing methods that rely on additional discriminator networks and unstable adversarial objectives. Furthermore, we present a new sampler architecture that, for the first time, enables implicit distributions over millions of latent variables, addressing computational concerns by using differentiable numerical approximations. Our empirical analysis indicates our method is capable of recovering correlations across layers in large Bayesian neural networks, a property that is crucial for a network's performance but notoriously challenging to achieve. To the best of our knowledge, no other method has been shown to accomplish this task for such large models. Through experiments in downstream tasks, we demonstrate that our expressive posteriors outperform state-of-the-art uncertainty quantification methods, validating the effectiveness of our training algorithm and the quality of the learned implicit approximation.

Adaptive Cholesky Gaussian Processes

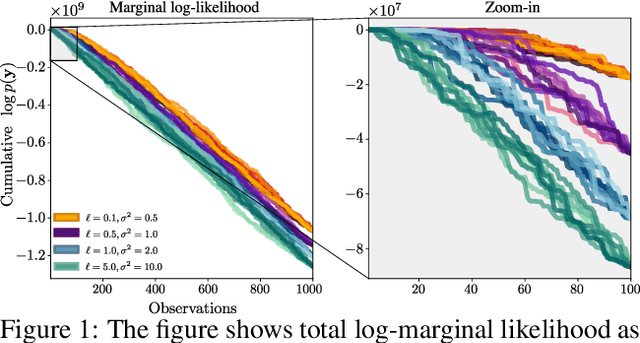
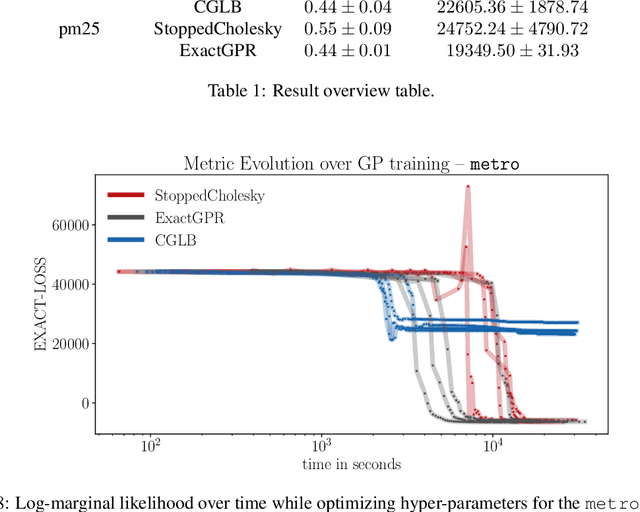
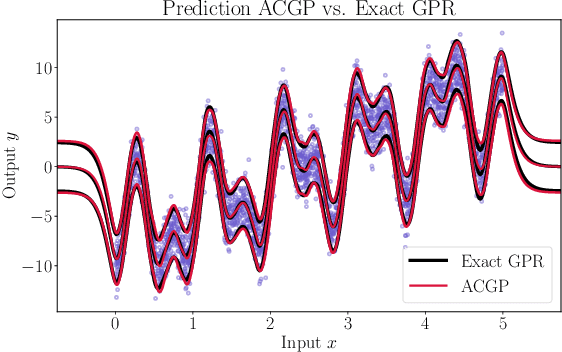
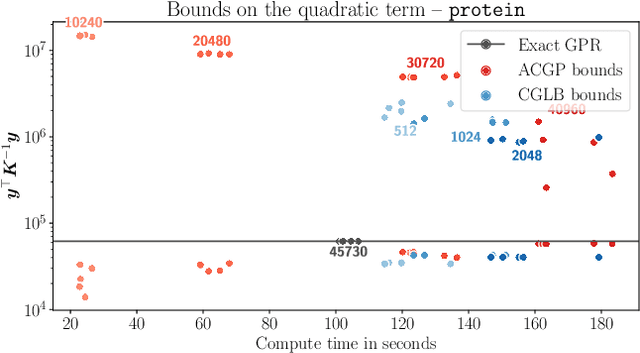
We present a method to fit exact Gaussian process models to large datasets by considering only a subset of the data. Our approach is novel in that the size of the subset is selected on the fly during exact inference with little computational overhead. From an empirical observation that the log-marginal likelihood often exhibits a linear trend once a sufficient subset of a dataset has been observed, we conclude that many large datasets contain redundant information that only slightly affects the posterior. Based on this, we provide probabilistic bounds on the full model evidence that can identify such subsets. Remarkably, these bounds are largely composed of terms that appear in intermediate steps of the standard Cholesky decomposition, allowing us to modify the algorithm to adaptively stop the decomposition once enough data have been observed. Empirically, we show that our method can be directly plugged into well-known inference schemes to fit exact Gaussian process models to large datasets.

Sacrificing information for the greater good: how to select photometric bands for optimal accuracy

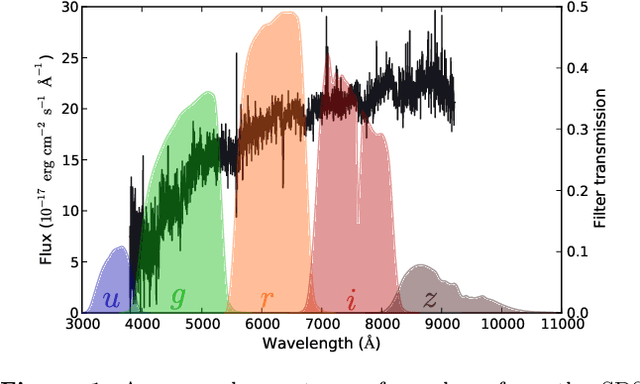
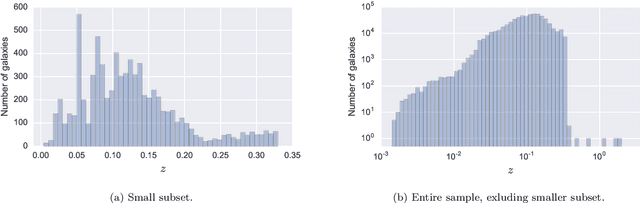
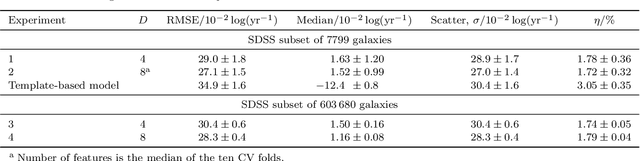
Large-scale surveys make huge amounts of photometric data available. Because of the sheer amount of objects, spectral data cannot be obtained for all of them. Therefore it is important to devise techniques for reliably estimating physical properties of objects from photometric information alone. These estimates are needed to automatically identify interesting objects worth a follow-up investigation as well as to produce the required data for a statistical analysis of the space covered by a survey. We argue that machine learning techniques are suitable to compute these estimates accurately and efficiently. This study promotes a feature selection algorithm, which selects the most informative magnitudes and colours for a given task of estimating physical quantities from photometric data alone. Using k nearest neighbours regression, a well-known non-parametric machine learning method, we show that using the found features significantly increases the accuracy of the estimations compared to using standard features and standard methods. We illustrate the usefulness of the approach by estimating specific star formation rates (sSFRs) and redshifts (photo-z's) using only the broad-band photometry from the Sloan Digital Sky Survey (SDSS). For estimating sSFRs, we demonstrate that our method produces better estimates than traditional spectral energy distribution (SED) fitting. For estimating photo-z's, we show that our method produces more accurate photo-z's than the method employed by SDSS. The study highlights the general importance of performing proper model selection to improve the results of machine learning systems and how feature selection can provide insights into the predictive relevance of particular input features.