Krista Gile
Selective Harvesting over Networks
Mar 15, 2017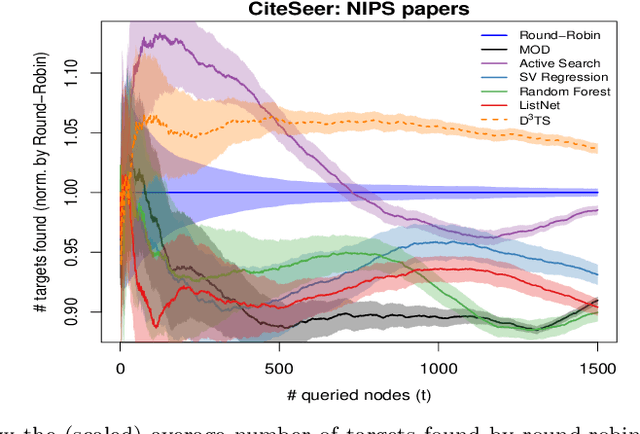

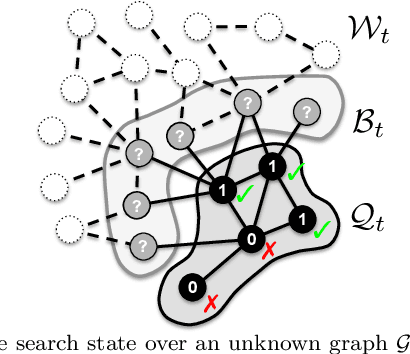
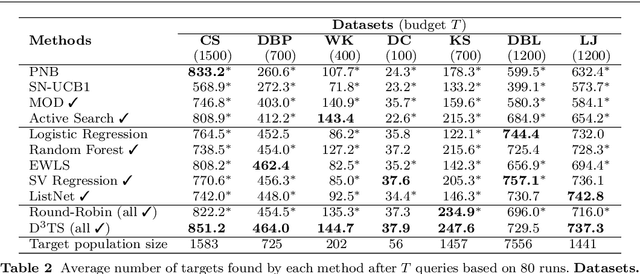
Abstract:Active search (AS) on graphs focuses on collecting certain labeled nodes (targets) given global knowledge of the network topology and its edge weights under a query budget. However, in most networks, nodes, topology and edge weights are all initially unknown. We introduce selective harvesting, a variant of AS where the next node to be queried must be chosen among the neighbors of the current queried node set; the available training data for deciding which node to query is restricted to the subgraph induced by the queried set (and their node attributes) and their neighbors (without any node or edge attributes). Therefore, selective harvesting is a sequential decision problem, where we must decide which node to query at each step. A classifier trained in this scenario suffers from a tunnel vision effect: without recourse to independent sampling, the urge to query promising nodes forces classifiers to gather increasingly biased training data, which we show significantly hurts the performance of AS methods and standard classifiers. We find that it is possible to collect a much larger set of targets by using multiple classifiers, not by combining their predictions as an ensemble, but switching between classifiers used at each step, as a way to ease the tunnel vision effect. We discover that switching classifiers collects more targets by (a) diversifying the training data and (b) broadening the choices of nodes that can be queried next. This highlights an exploration, exploitation, and diversification trade-off in our problem that goes beyond the exploration and exploitation duality found in classic sequential decision problems. From these observations we propose D3TS, a method based on multi-armed bandits for non-stationary stochastic processes that enforces classifier diversity, matching or exceeding the performance of competing methods on seven real network datasets in our evaluation.
Learning to Generate Networks
Nov 10, 2014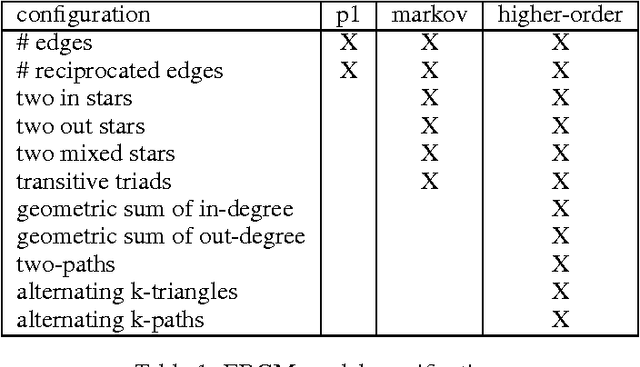
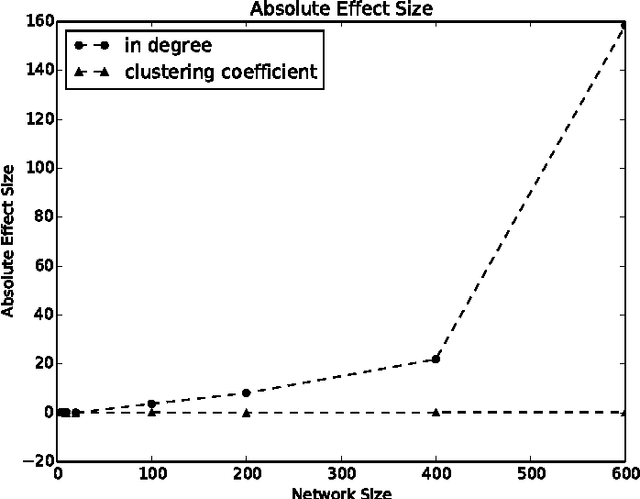
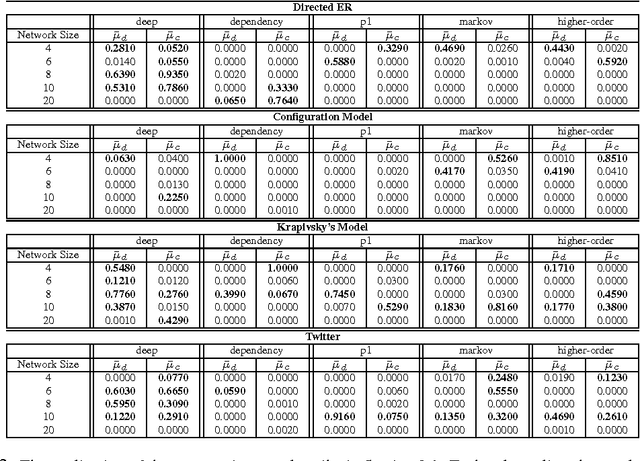
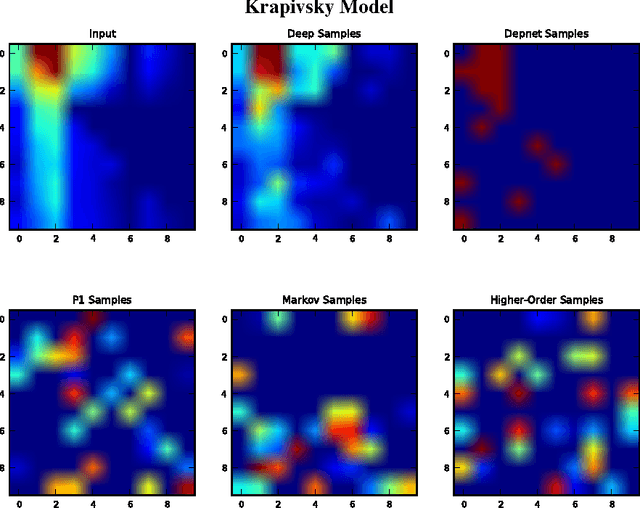
Abstract:We investigate the problem of learning to generate complex networks from data. Specifically, we consider whether deep belief networks, dependency networks, and members of the exponential random graph family can learn to generate networks whose complex behavior is consistent with a set of input examples. We find that the deep model is able to capture the complex behavior of small networks, but that no model is able capture this behavior for networks with more than a handful of nodes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge