FluTO: Graded Multiscale Fluid Topology Optimization using Neural Networks

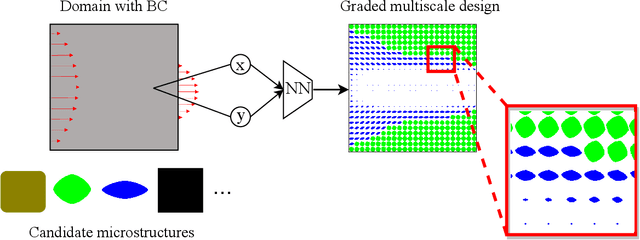
Fluid-flow devices with low dissipation, but high contact area, are of importance in many applications. A well-known strategy to design such devices is multi-scale topology optimization (MTO), where optimal microstructures are designed within each cell of a discretized domain. Unfortunately, MTO is computationally very expensive since one must perform homogenization of the evolving microstructures, during each step of the homogenization process. As an alternate, we propose here a graded multiscale topology optimization (GMTO) for designing fluid-flow devices. In the proposed method, several pre-selected but size-parameterized and orientable microstructures are used to fill the domain optimally. GMTO significantly reduces the computation while retaining many of the benefits of MTO. In particular, GMTO is implemented here using a neural-network (NN) since: (1) homogenization can be performed off-line, and used by the NN during optimization, (2) it enables continuous switching between microstructures during optimization, (3) the number of design variables and computational effort is independent of number of microstructure used, and, (4) it supports automatic differentiation, thereby eliminating manual sensitivity analysis. Several numerical results are presented to illustrate the proposed framework.

A Generalized Framework for Microstructural Optimization using Neural Networks

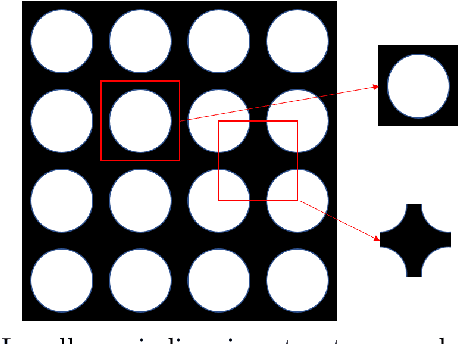
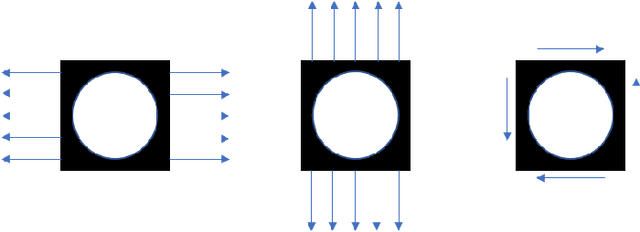
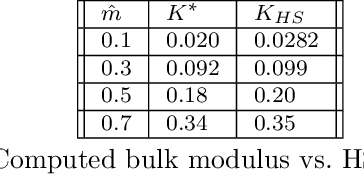
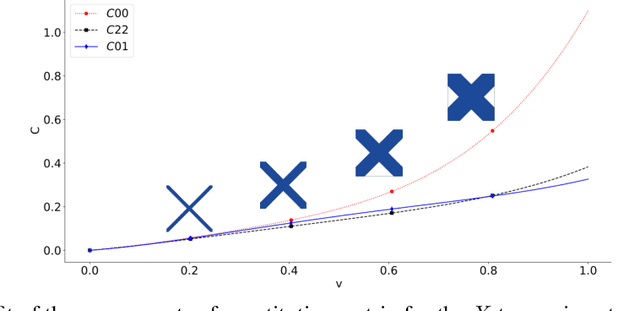
Microstructures, i.e., architected materials, are designed today, typically, by maximizing an objective, such as bulk modulus, subject to a volume constraint. However, in many applications, it is often more appropriate to impose constraints on other physical quantities of interest. In this paper, we consider such generalized microstructural optimization problems where any of the microstructural quantities, namely, bulk, shear, Poisson ratio, or volume, can serve as the objective, while the remaining can serve as constraints. In particular, we propose here a neural-network (NN) framework to solve such problems. The framework relies on the classic density formulation of microstructural optimization, but the density field is represented through the NN's weights and biases. The main characteristics of the proposed NN framework are: (1) it supports automatic differentiation, eliminating the need for manual sensitivity derivations, (2) smoothing filters are not required due to implicit filtering, (3) the framework can be easily extended to multiple-materials, and (4) a high-resolution microstructural topology can be recovered through a simple post-processing step. The framework is illustrated through a variety of microstructural optimization problems.

FRC-TOuNN: Topology Optimization of Continuous Fiber Reinforced Composites using Neural Network

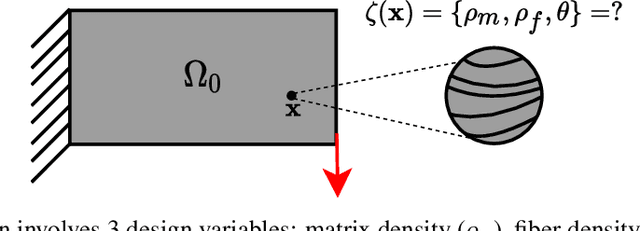
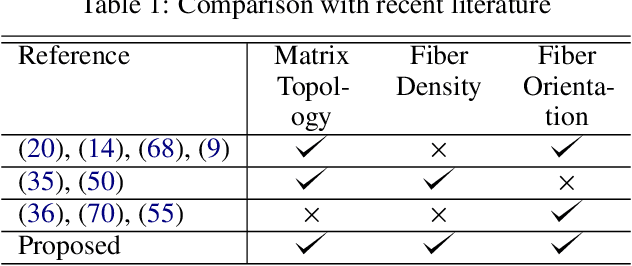
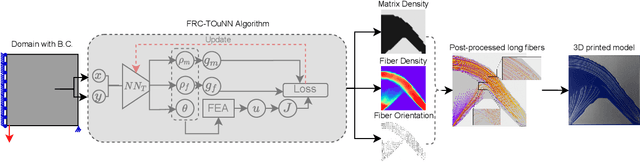
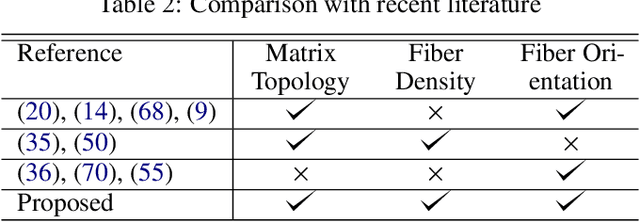
In this paper, we present a topology optimization (TO) framework to simultaneously optimize the matrix topology and fiber distribution of functionally graded continuous fiber-reinforced composites (FRC). Current approaches in density-based TO for FRC use the underlying finite element mesh both for analysis and design representation. This poses several limitations while enforcing sub-element fiber spacing and generating high-resolution continuous fibers. In contrast, we propose a mesh-independent representation based on a neural network (NN) both to capture the matrix topology and fiber distribution. The implicit NN-based representation enables geometric and material queries at a higher resolution than a mesh discretization. This leads to the accurate extraction of functionally-graded continuous fibers. Further, by integrating the finite element simulations into the NN computational framework, we can leverage automatic differentiation for end-to-end automated sensitivity analysis, i.e., we no longer need to manually derive cumbersome sensitivity expressions. We demonstrate the effectiveness and computational efficiency of the proposed method through several numerical examples involving various objective functions. We also show that the optimized continuous fiber reinforced composites can be directly fabricated at high resolution using additive manufacturing.

GM-TOuNN: Graded Multiscale Topology Optimization using Neural Networks

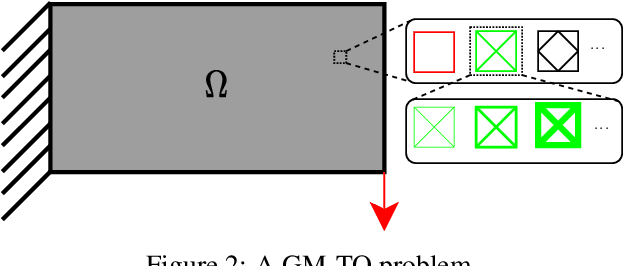
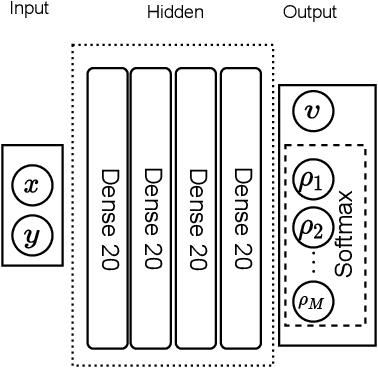
Multiscale topology optimization (M-TO) entails generating an optimal global topology, and an optimal set of microstructures at a smaller scale, for a physics-constrained problem. With the advent of additive manufacturing, M-TO has gained significant prominence. However, generating optimal microstructures at various locations can be computationally very expensive. As an alternate, graded multiscale topology optimization (GM-TO) has been proposed where one or more pre-selected and graded (parameterized) microstructural topologies are used to fill the domain optimally. This leads to a significant reduction in computation while retaining many of the benefits of M-TO. A successful GM-TO framework must: (1) be capable of efficiently handling numerous pre-selected microstructures, (2) be able to continuously switch between these microstructures during optimization, (3) ensure that the partition of unity is satisfied, and (4) discourage microstructure mixing at termination. In this paper, we propose to meet these requirements by exploiting the unique classification capacity of neural networks. Specifically, we propose a graded multiscale topology optimization using neural-network (GM-TOuNN) framework with the following features: (1) the number of design variables is only weakly dependent on the number of pre-selected microstructures, (2) it guarantees partition of unity while discouraging microstructure mixing, and (3) it supports automatic differentiation, thereby eliminating manual sensitivity analysis. The proposed framework is illustrated through several examples.

Integrating Material Selection with Design Optimization via Neural Networks

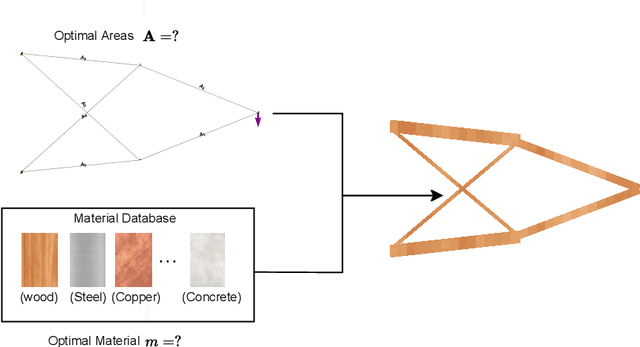
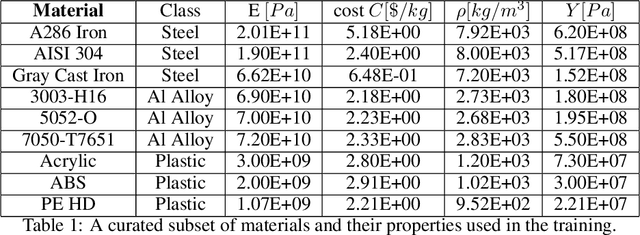
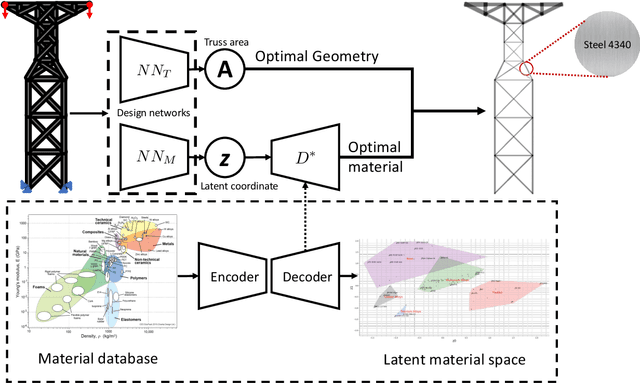
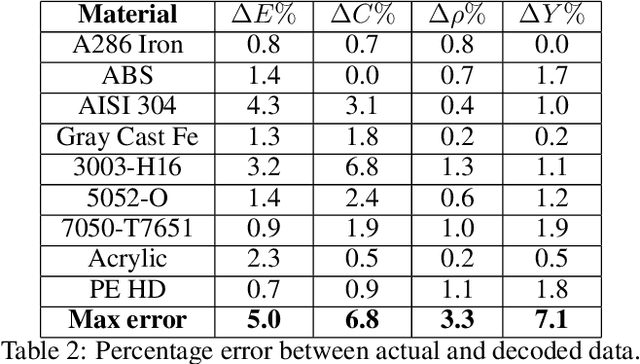
The engineering design process often entails optimizing the underlying geometry while simultaneously selecting a suitable material. For a certain class of simple problems, the two are separable where, for example, one can first select an optimal material, and then optimize the geometry. However, in general, the two are not separable. Furthermore, the discrete nature of material selection is not compatible with gradient-based geometry optimization, making simultaneous optimization challenging. In this paper, we propose the use of variational autoencoders (VAE) for simultaneous optimization. First, a data-driven VAE is used to project the discrete material database onto a continuous and differentiable latent space. This is then coupled with a fully-connected neural network, embedded with a finite-element solver, to simultaneously optimize the material and geometry. The neural-network's built-in gradient optimizer and back-propagation are exploited during optimization. The proposed framework is demonstrated using trusses, where an optimal material needs to be chosen from a database, while simultaneously optimizing the cross-sectional areas of the truss members. Several numerical examples illustrate the efficacy of the proposed framework. The Python code used in these experiments is available at github.com/UW-ERSL/MaTruss

Randomized Algorithms for Large scale SVMs

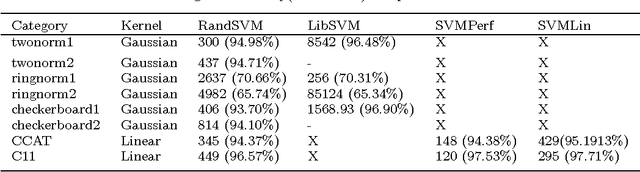
We propose a randomized algorithm for training Support vector machines(SVMs) on large datasets. By using ideas from Random projections we show that the combinatorial dimension of SVMs is $O({log} n)$ with high probability. This estimate of combinatorial dimension is used to derive an iterative algorithm, called RandSVM, which at each step calls an existing solver to train SVMs on a randomly chosen subset of size $O({log} n)$. The algorithm has probabilistic guarantees and is capable of training SVMs with Kernels for both classification and regression problems. Experiments done on synthetic and real life data sets demonstrate that the algorithm scales up existing SVM learners, without loss of accuracy.