Deep Neural Implicit Representation of Accessibility for Multi-Axis Manufacturing

One of the main concerns in design and process planning for multi-axis additive and subtractive manufacturing is collision avoidance between moving objects (e.g., tool assemblies) and stationary objects (e.g., a part unified with fixtures). The collision measure for various pairs of relative rigid translations and rotations between the two pointsets can be conceptualized by a compactly supported scalar field over the 6D non-Euclidean configuration space. Explicit representation and computation of this field is costly in both time and space. If we fix $O(m)$ sparsely sampled rotations (e.g., tool orientations), computation of the collision measure field as a convolution of indicator functions of the 3D pointsets over a uniform grid (i.e., voxelized geometry) of resolution $O(n^3)$ via fast Fourier transforms (FFTs) scales as in $O(mn^3 \log n)$ in time and $O(mn^3)$ in space. In this paper, we develop an implicit representation of the collision measure field via deep neural networks (DNNs). We show that our approach is able to accurately interpolate the collision measure from a sparse sampling of rotations, and can represent the collision measure field with a small memory footprint. Moreover, we show that this representation can be efficiently updated through fine-tuning to more efficiently train the network on multi-resolution data, as well as accommodate incremental changes to the geometry (such as might occur in iterative processes such as topology optimization of the part subject to CNC tool accessibility constraints).

FRC-TOuNN: Topology Optimization of Continuous Fiber Reinforced Composites using Neural Network

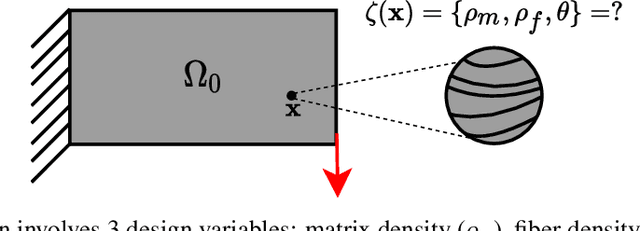
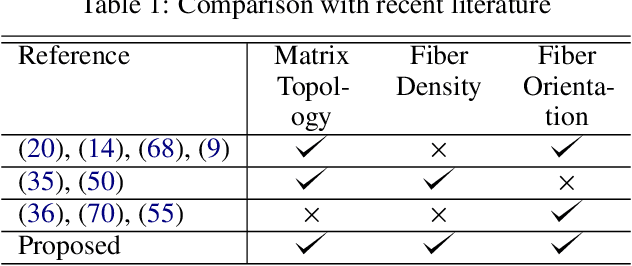
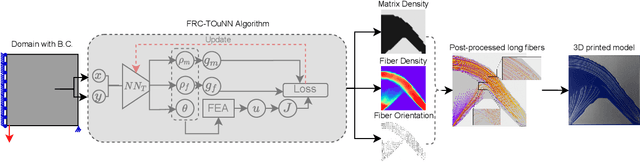
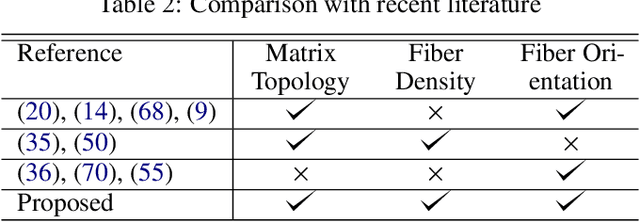
In this paper, we present a topology optimization (TO) framework to simultaneously optimize the matrix topology and fiber distribution of functionally graded continuous fiber-reinforced composites (FRC). Current approaches in density-based TO for FRC use the underlying finite element mesh both for analysis and design representation. This poses several limitations while enforcing sub-element fiber spacing and generating high-resolution continuous fibers. In contrast, we propose a mesh-independent representation based on a neural network (NN) both to capture the matrix topology and fiber distribution. The implicit NN-based representation enables geometric and material queries at a higher resolution than a mesh discretization. This leads to the accurate extraction of functionally-graded continuous fibers. Further, by integrating the finite element simulations into the NN computational framework, we can leverage automatic differentiation for end-to-end automated sensitivity analysis, i.e., we no longer need to manually derive cumbersome sensitivity expressions. We demonstrate the effectiveness and computational efficiency of the proposed method through several numerical examples involving various objective functions. We also show that the optimized continuous fiber reinforced composites can be directly fabricated at high resolution using additive manufacturing.