A Generalized Framework for Microstructural Optimization using Neural Networks

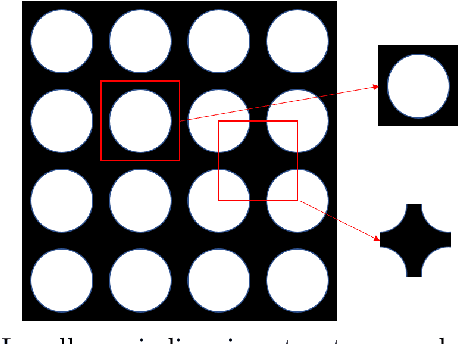
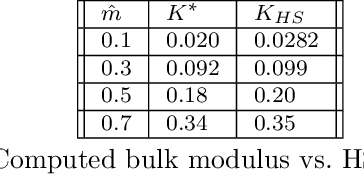
Microstructures, i.e., architected materials, are designed today, typically, by maximizing an objective, such as bulk modulus, subject to a volume constraint. However, in many applications, it is often more appropriate to impose constraints on other physical quantities of interest. In this paper, we consider such generalized microstructural optimization problems where any of the microstructural quantities, namely, bulk, shear, Poisson ratio, or volume, can serve as the objective, while the remaining can serve as constraints. In particular, we propose here a neural-network (NN) framework to solve such problems. The framework relies on the classic density formulation of microstructural optimization, but the density field is represented through the NN's weights and biases. The main characteristics of the proposed NN framework are: (1) it supports automatic differentiation, eliminating the need for manual sensitivity derivations, (2) smoothing filters are not required due to implicit filtering, (3) the framework can be easily extended to multiple-materials, and (4) a high-resolution microstructural topology can be recovered through a simple post-processing step. The framework is illustrated through a variety of microstructural optimization problems.

GM-TOuNN: Graded Multiscale Topology Optimization using Neural Networks

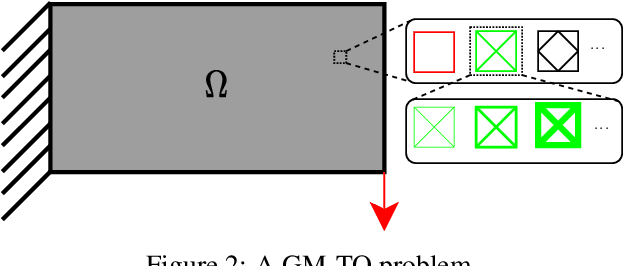
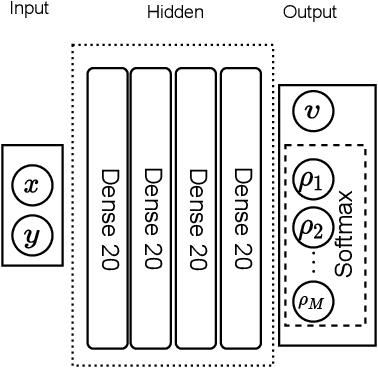
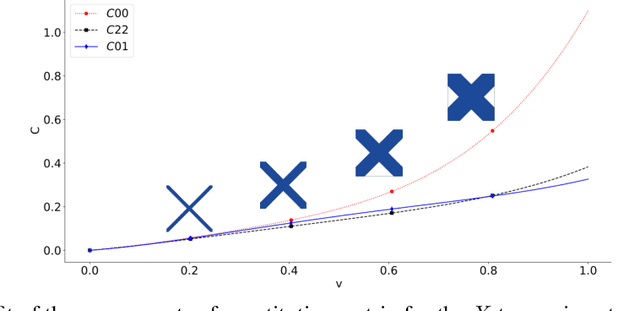
Multiscale topology optimization (M-TO) entails generating an optimal global topology, and an optimal set of microstructures at a smaller scale, for a physics-constrained problem. With the advent of additive manufacturing, M-TO has gained significant prominence. However, generating optimal microstructures at various locations can be computationally very expensive. As an alternate, graded multiscale topology optimization (GM-TO) has been proposed where one or more pre-selected and graded (parameterized) microstructural topologies are used to fill the domain optimally. This leads to a significant reduction in computation while retaining many of the benefits of M-TO. A successful GM-TO framework must: (1) be capable of efficiently handling numerous pre-selected microstructures, (2) be able to continuously switch between these microstructures during optimization, (3) ensure that the partition of unity is satisfied, and (4) discourage microstructure mixing at termination. In this paper, we propose to meet these requirements by exploiting the unique classification capacity of neural networks. Specifically, we propose a graded multiscale topology optimization using neural-network (GM-TOuNN) framework with the following features: (1) the number of design variables is only weakly dependent on the number of pre-selected microstructures, (2) it guarantees partition of unity while discouraging microstructure mixing, and (3) it supports automatic differentiation, thereby eliminating manual sensitivity analysis. The proposed framework is illustrated through several examples.

Integrating Material Selection with Design Optimization via Neural Networks

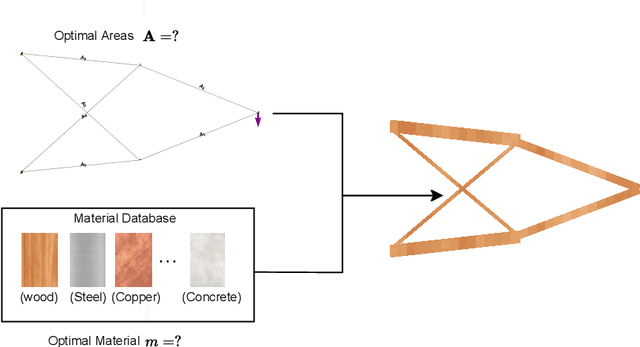
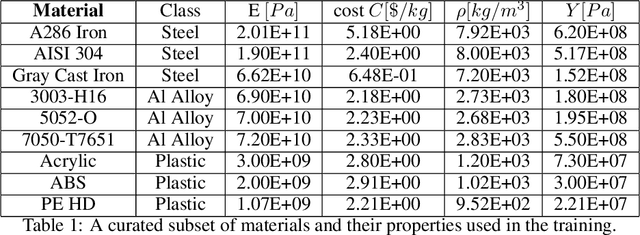
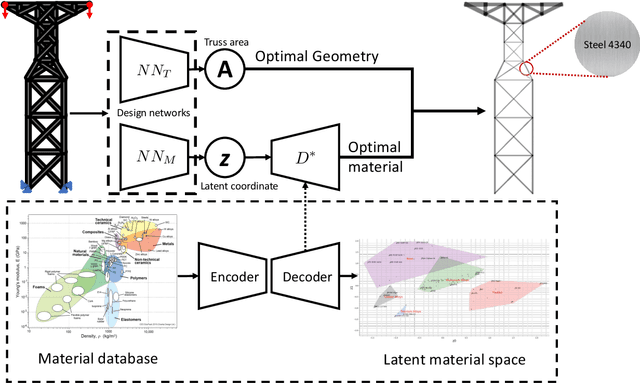
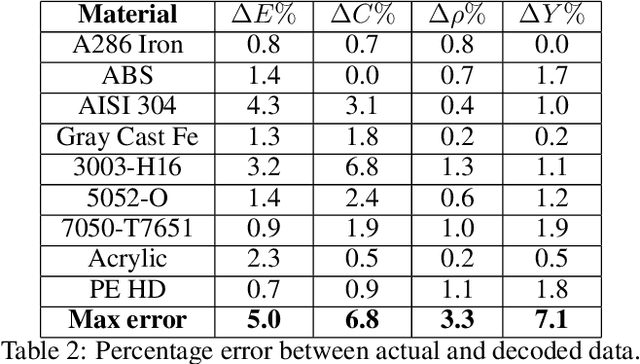
The engineering design process often entails optimizing the underlying geometry while simultaneously selecting a suitable material. For a certain class of simple problems, the two are separable where, for example, one can first select an optimal material, and then optimize the geometry. However, in general, the two are not separable. Furthermore, the discrete nature of material selection is not compatible with gradient-based geometry optimization, making simultaneous optimization challenging. In this paper, we propose the use of variational autoencoders (VAE) for simultaneous optimization. First, a data-driven VAE is used to project the discrete material database onto a continuous and differentiable latent space. This is then coupled with a fully-connected neural network, embedded with a finite-element solver, to simultaneously optimize the material and geometry. The neural-network's built-in gradient optimizer and back-propagation are exploited during optimization. The proposed framework is demonstrated using trusses, where an optimal material needs to be chosen from a database, while simultaneously optimizing the cross-sectional areas of the truss members. Several numerical examples illustrate the efficacy of the proposed framework. The Python code used in these experiments is available at github.com/UW-ERSL/MaTruss