Vinay Jethava
On weighted uncertainty sampling in active learning
Sep 11, 2019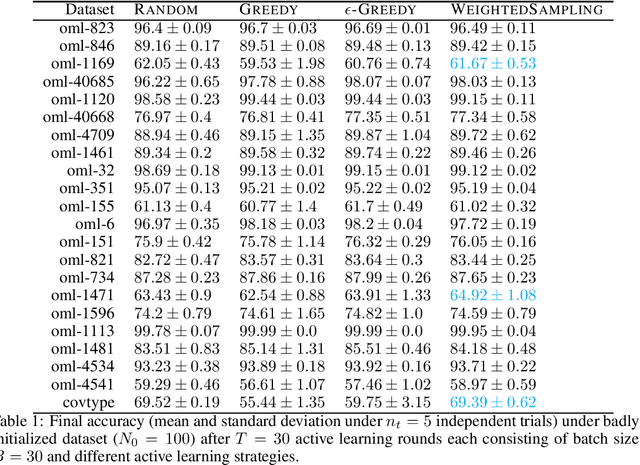
Abstract:This note explores probabilistic sampling weighted by uncertainty in active learning. This method has been previously used and authors have tangentially remarked on its efficacy. The scheme has several benefits: (1) it is computationally cheap, (2) it can be implemented in a single-pass streaming fashion which is a benefit when deployed in real-world systems where different subsystems perform the suggestion scoring and extraction of user feedback, and (3) it is easily parameterizable. In this paper, we show on publicly available datasets that using probabilistic weighting is often beneficial and strikes a good compromise between exploration and representation especially when the starting set of labelled points is biased.
Easy High-Dimensional Likelihood-Free Inference
Aug 23, 2018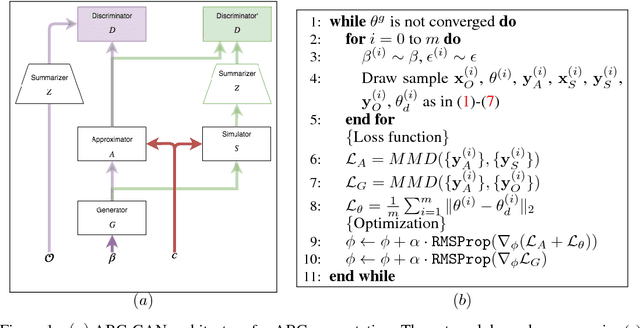
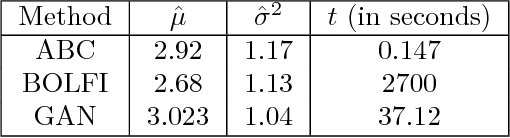
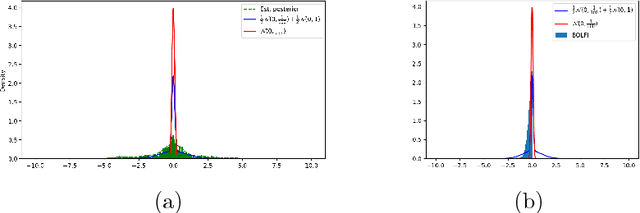

Abstract:We introduce a framework using Generative Adversarial Networks (GANs) for likelihood--free inference (LFI) and Approximate Bayesian Computation (ABC) where we replace the black-box simulator model with an approximator network and generate a rich set of summary features in a data driven fashion. On benchmark data sets, our approach improves on others with respect to scalability, ability to handle high dimensional data and complex probability distributions.
Extension of Path Probability Method to Approximate Inference over Time
Sep 19, 2009
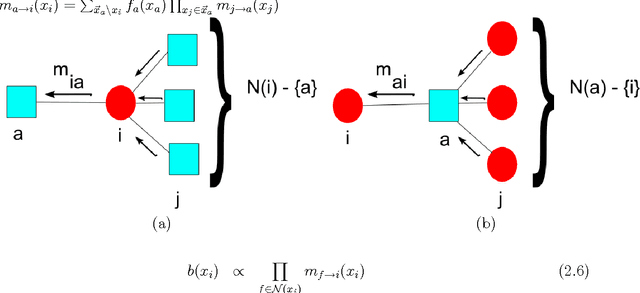
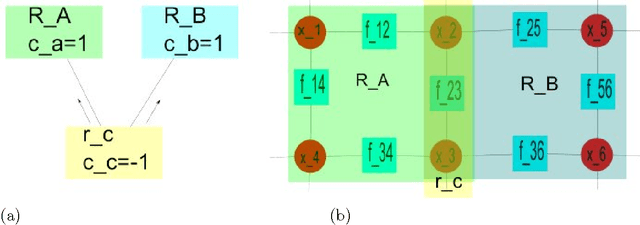
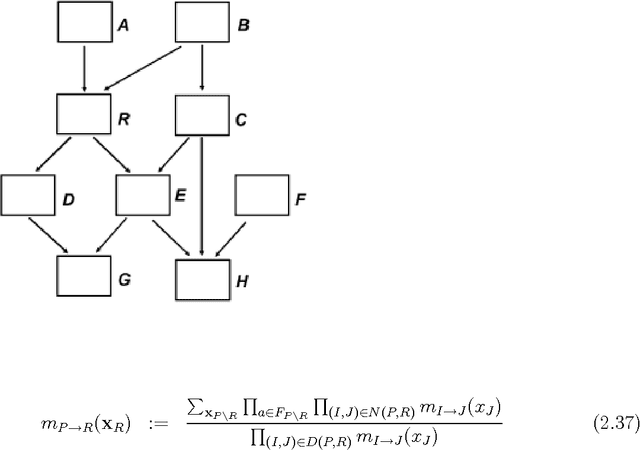
Abstract:There has been a tremendous growth in publicly available digital video footage over the past decade. This has necessitated the development of new techniques in computer vision geared towards efficient analysis, storage and retrieval of such data. Many mid-level computer vision tasks such as segmentation, object detection, tracking, etc. involve an inference problem based on the video data available. Video data has a high degree of spatial and temporal coherence. The property must be intelligently leveraged in order to obtain better results. Graphical models, such as Markov Random Fields, have emerged as a powerful tool for such inference problems. They are naturally suited for expressing the spatial dependencies present in video data, It is however, not clear, how to extend the existing techniques for the problem of inference over time. This thesis explores the Path Probability Method, a variational technique in statistical mechanics, in the context of graphical models and approximate inference problems. It extends the method to a general framework for problems involving inference in time, resulting in an algorithm, \emph{DynBP}. We explore the relation of the algorithm with existing techniques, and find the algorithm competitive with existing approaches. The main contribution of this thesis are the extended GBP algorithm, the extension of Path Probability Methods to the DynBP algorithm and the relationship between them. We have also explored some applications in computer vision involving temporal evolution with promising results.
Randomized Algorithms for Large scale SVMs
Sep 19, 2009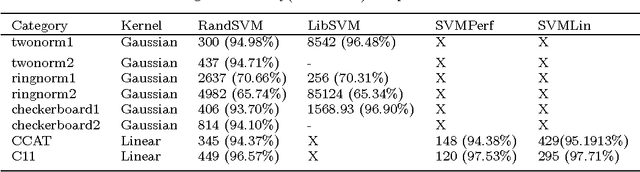

Abstract:We propose a randomized algorithm for training Support vector machines(SVMs) on large datasets. By using ideas from Random projections we show that the combinatorial dimension of SVMs is $O({log} n)$ with high probability. This estimate of combinatorial dimension is used to derive an iterative algorithm, called RandSVM, which at each step calls an existing solver to train SVMs on a randomly chosen subset of size $O({log} n)$. The algorithm has probabilistic guarantees and is capable of training SVMs with Kernels for both classification and regression problems. Experiments done on synthetic and real life data sets demonstrate that the algorithm scales up existing SVM learners, without loss of accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge