Extension of Path Probability Method to Approximate Inference over Time

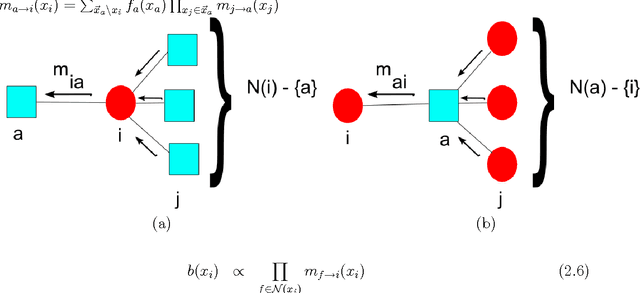
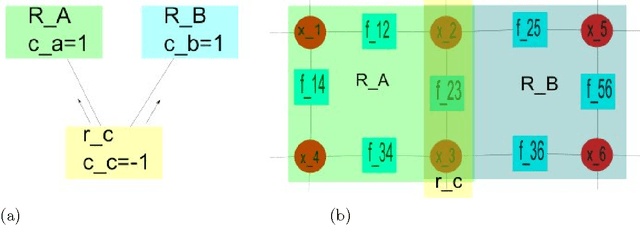
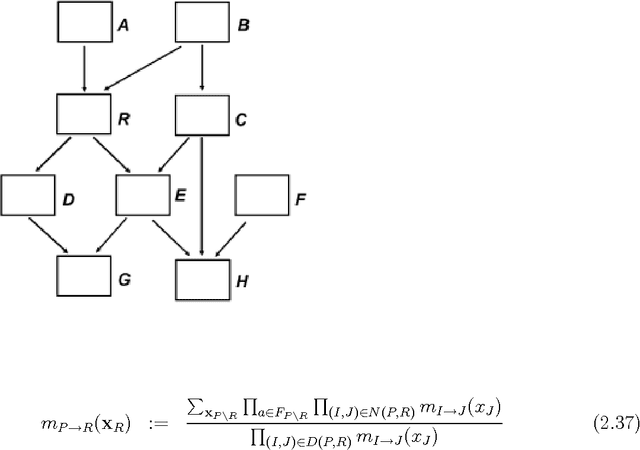
There has been a tremendous growth in publicly available digital video footage over the past decade. This has necessitated the development of new techniques in computer vision geared towards efficient analysis, storage and retrieval of such data. Many mid-level computer vision tasks such as segmentation, object detection, tracking, etc. involve an inference problem based on the video data available. Video data has a high degree of spatial and temporal coherence. The property must be intelligently leveraged in order to obtain better results. Graphical models, such as Markov Random Fields, have emerged as a powerful tool for such inference problems. They are naturally suited for expressing the spatial dependencies present in video data, It is however, not clear, how to extend the existing techniques for the problem of inference over time. This thesis explores the Path Probability Method, a variational technique in statistical mechanics, in the context of graphical models and approximate inference problems. It extends the method to a general framework for problems involving inference in time, resulting in an algorithm, \emph{DynBP}. We explore the relation of the algorithm with existing techniques, and find the algorithm competitive with existing approaches. The main contribution of this thesis are the extended GBP algorithm, the extension of Path Probability Methods to the DynBP algorithm and the relationship between them. We have also explored some applications in computer vision involving temporal evolution with promising results.