Kiattikun Chobtham
Leveraging Teleconnections with Physics-Informed Graph Attention Networks for Long-Range Extreme Rainfall Forecasting in Thailand
Oct 14, 2025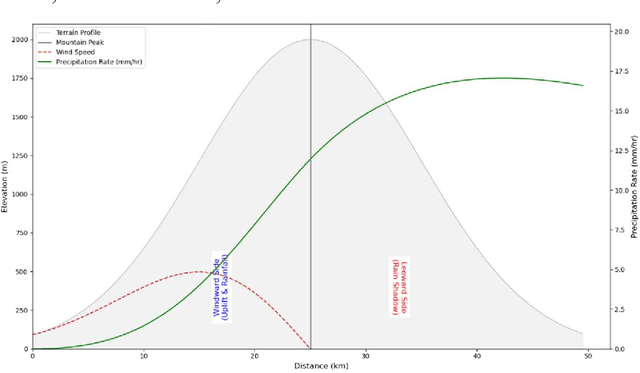

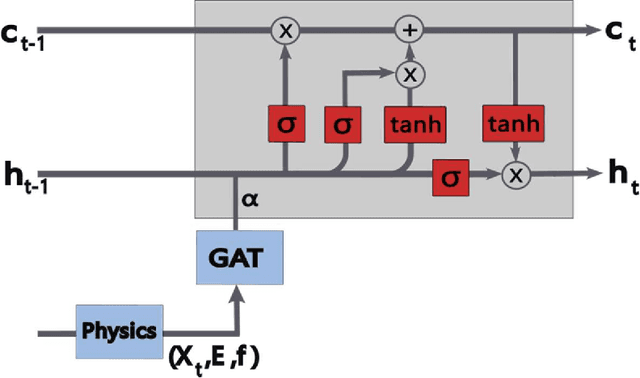
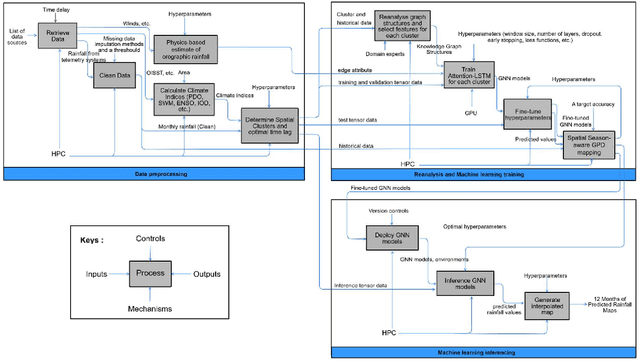
Abstract:Accurate rainfall forecasting, particularly for extreme events, remains a significant challenge in climatology and the Earth system. This paper presents novel physics-informed Graph Neural Networks (GNNs) combined with extreme-value analysis techniques to improve gauge-station rainfall predictions across Thailand. The model leverages a graph-structured representation of gauge stations to capture complex spatiotemporal patterns, and it offers explainability through teleconnections. We preprocess relevant climate indices that potentially influence regional rainfall. The proposed Graph Attention Network with Long Short-Term Memory (Attention-LSTM) applies the attention mechanism using initial edge features derived from simple orographic-precipitation physics formulation. The embeddings are subsequently processed by LSTM layers. To address extremes, we perform Peak-Over-Threshold (POT) mapping using the novel Spatial Season-aware Generalized Pareto Distribution (GPD) method, which overcomes limitations of traditional machine-learning models. Experiments demonstrate that our method outperforms well-established baselines across most regions, including areas prone to extremes, and remains strongly competitive with the state of the art. Compared with the operational forecasting system SEAS5, our real-world application improves extreme-event prediction and offers a practical enhancement to produce fine-resolution maps that support decision-making in long-term water management.
Tuning structure learning algorithms with out-of-sample and resampling strategies
Jun 24, 2023Abstract:One of the challenges practitioners face when applying structure learning algorithms to their data involves determining a set of hyperparameters; otherwise, a set of hyperparameter defaults is assumed. The optimal hyperparameter configuration often depends on multiple factors, including the size and density of the usually unknown underlying true graph, the sample size of the input data, and the structure learning algorithm. We propose a novel hyperparameter tuning method, called the Out-of-sample Tuning for Structure Learning (OTSL), that employs out-of-sample and resampling strategies to estimate the optimal hyperparameter configuration for structure learning, given the input data set and structure learning algorithm. Synthetic experiments show that employing OTSL as a means to tune the hyperparameters of hybrid and score-based structure learning algorithms leads to improvements in graphical accuracy compared to the state-of-the-art. We also illustrate the applicability of this approach to real datasets from different disciplines.
Open problems in causal structure learning: A case study of COVID-19 in the UK
May 05, 2023Abstract:Causal machine learning (ML) algorithms recover graphical structures that tell us something about cause-and-effect relationships. The causal representation provided by these algorithms enables transparency and explainability, which is necessary in critical real-world problems. Yet, causal ML has had limited impact in practice compared to associational ML. This paper investigates the challenges of causal ML with application to COVID-19 UK pandemic data. We collate data from various public sources and investigate what the various structure learning algorithms learn from these data. We explore the impact of different data formats on algorithms spanning different classes of learning, and assess the results produced by each algorithm, and groups of algorithms, in terms of graphical structure, model dimensionality, sensitivity analysis, confounding variables, predictive and interventional inference. We use these results to highlight open problems in causal structure learning and directions for future research. To facilitate future work, we make all graphs, models and data sets publicly available online.
Discovery and density estimation of latent confounders in Bayesian networks with evidence lower bound
Jun 16, 2022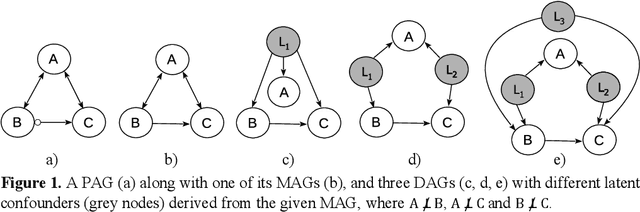

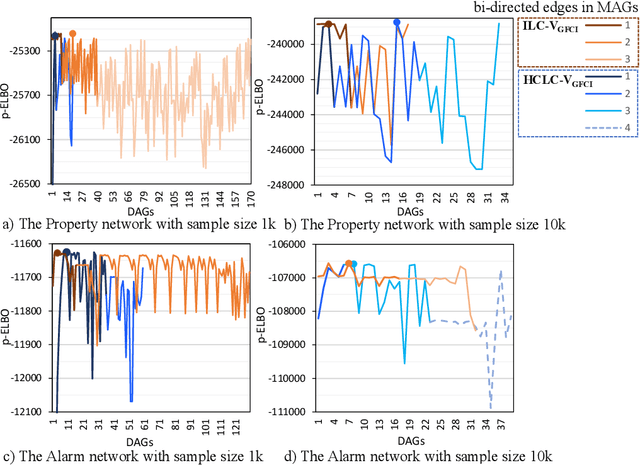
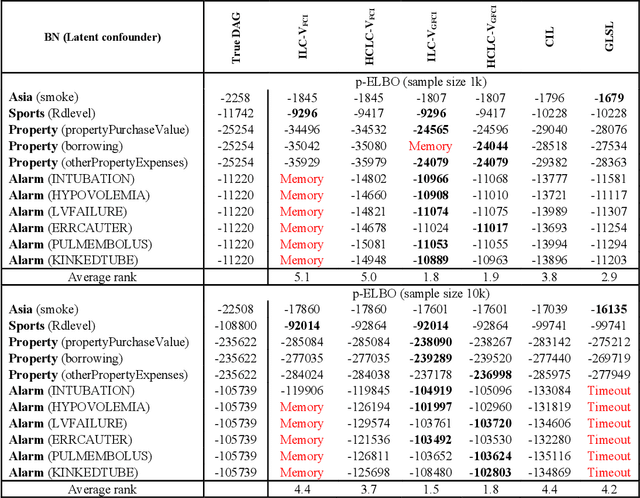
Abstract:Discovering and parameterising latent confounders represent important and challenging problems in causal structure learning and density estimation respectively. In this paper, we focus on both discovering and learning the distribution of latent confounders. This task requires solutions that come from different areas of statistics and machine learning. We combine elements of variational Bayesian methods, expectation-maximisation, hill-climbing search, and structure learning under the assumption of causal insufficiency. We propose two learning strategies; one that maximises model selection accuracy, and another that improves computational efficiency in exchange for minor reductions in accuracy. The former strategy is suitable for small networks and the latter for moderate size networks. Both learning strategies perform well relative to existing solutions.
Hybrid Bayesian network discovery with latent variables by scoring multiple interventions
Dec 20, 2021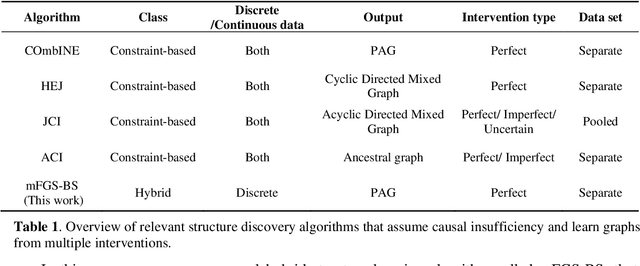
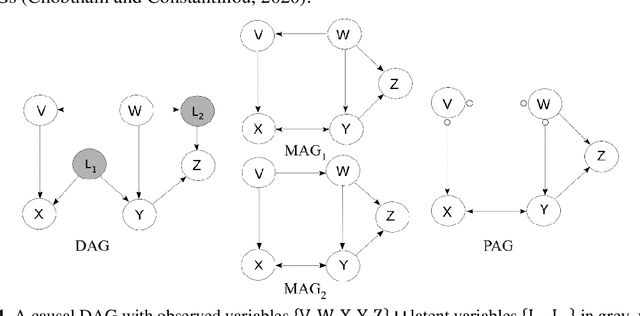
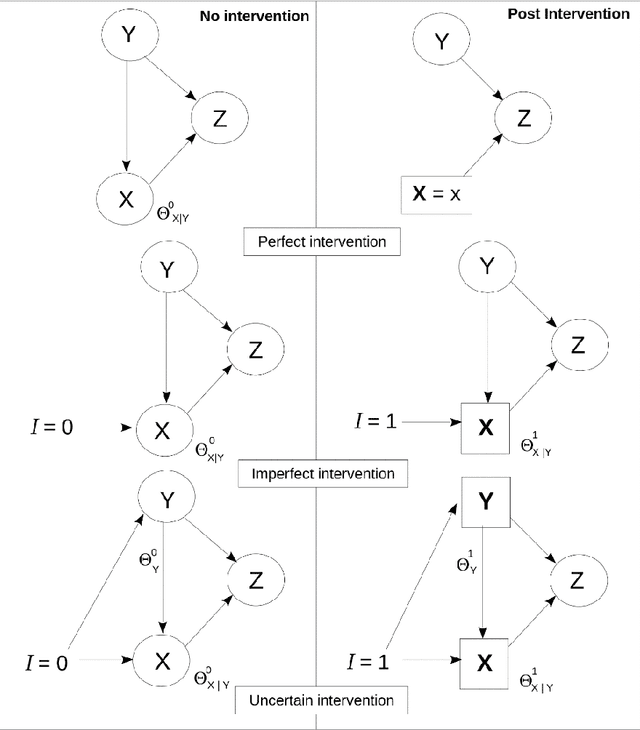

Abstract:In Bayesian Networks (BNs), the direction of edges is crucial for causal reasoning and inference. However, Markov equivalence class considerations mean it is not always possible to establish edge orientations, which is why many BN structure learning algorithms cannot orientate all edges from purely observational data. Moreover, latent confounders can lead to false positive edges. Relatively few methods have been proposed to address these issues. In this work, we present the hybrid mFGS-BS (majority rule and Fast Greedy equivalence Search with Bayesian Scoring) algorithm for structure learning from discrete data that involves an observational data set and one or more interventional data sets. The algorithm assumes causal insufficiency in the presence of latent variables and produces a Partial Ancestral Graph (PAG). Structure learning relies on a hybrid approach and a novel Bayesian scoring paradigm that calculates the posterior probability of each directed edge being added to the learnt graph. Experimental results based on well-known networks of up to 109 variables and 10k sample size show that mFGS-BS improves structure learning accuracy relative to the state-of-the-art and it is computationally efficient.
Effective and efficient structure learning with pruning and model averaging strategies
Dec 01, 2021
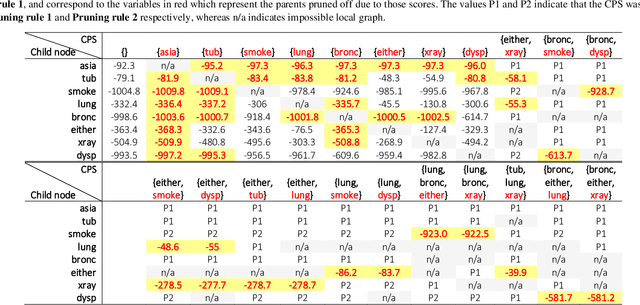
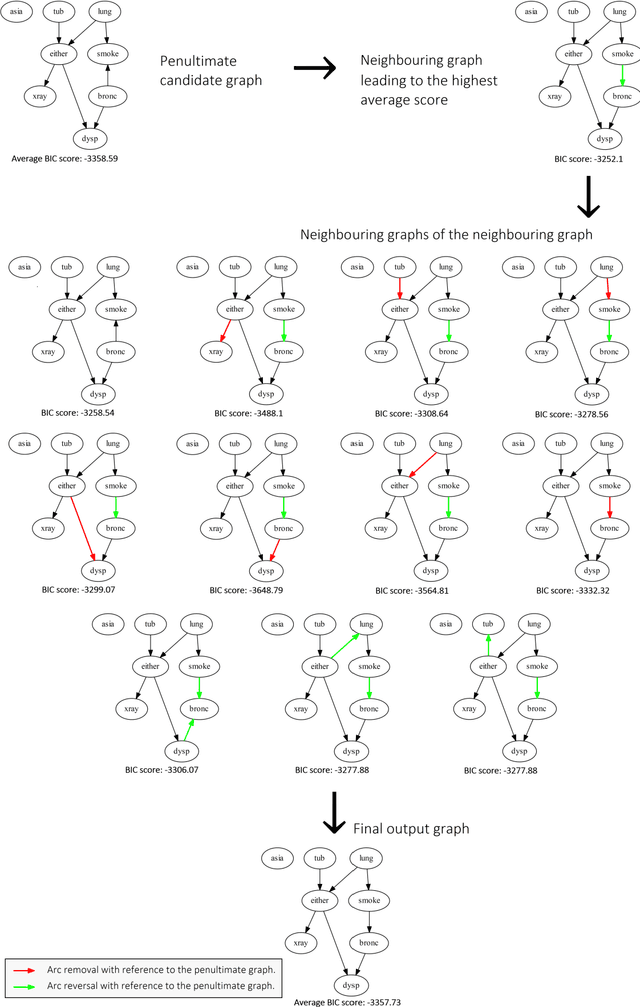
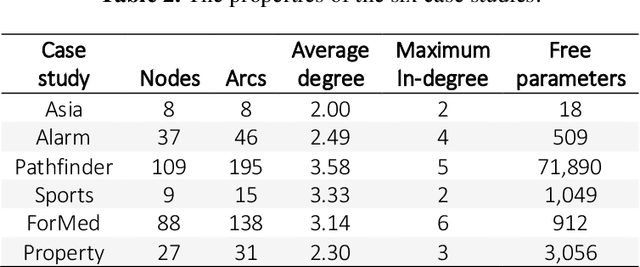
Abstract:Learning the structure of a Bayesian Network (BN) with score-based solutions involves exploring the search space of possible graphs and moving towards the graph that maximises a given objective function. Some algorithms offer exact solutions that guarantee to return the graph with the highest objective score, while others offer approximate solutions in exchange for reduced computational complexity. This paper describes an approximate BN structure learning algorithm, which we call Model Averaging Hill-Climbing (MAHC), that combines two novel strategies with hill-climbing search. The algorithm starts by pruning the search space of graphs, where the pruning strategy can be viewed as an aggressive version of the pruning strategies that are typically applied to combinatorial optimisation structure learning problems. It then performs model averaging in the hill-climbing search process and moves to the neighbouring graph that maximises the objective function, on average, for that neighbouring graph and over all its valid neighbouring graphs. Comparisons with other algorithms spanning different classes of learning suggest that the combination of aggressive pruning with model averaging is both effective and efficient, particularly in the presence of data noise.
A survey of Bayesian Network structure learning
Sep 23, 2021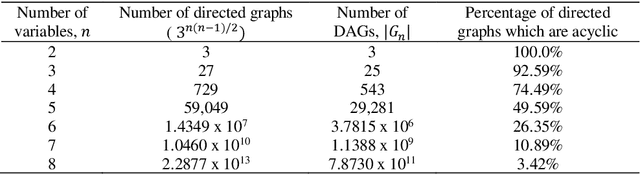

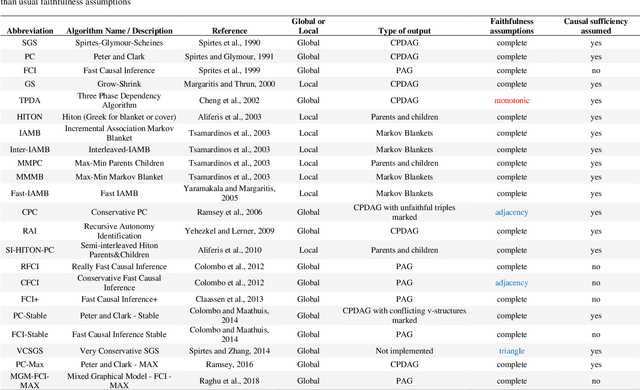
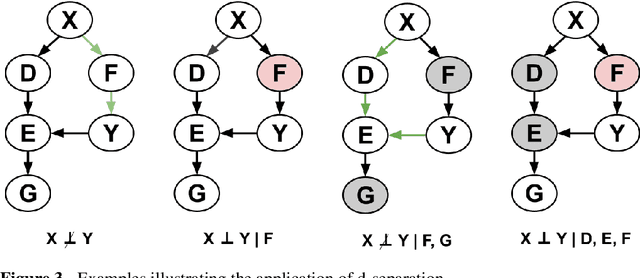
Abstract:Bayesian Networks (BNs) have become increasingly popular over the last few decades as a tool for reasoning under uncertainty in fields as diverse as medicine, biology, epidemiology, economics and the social sciences. This is especially true in real-world areas where we seek to answer complex questions based on hypothetical evidence to determine actions for intervention. However, determining the graphical structure of a BN remains a major challenge, especially when modelling a problem under causal assumptions. Solutions to this problem include the automated discovery of BN graphs from data, constructing them based on expert knowledge, or a combination of the two. This paper provides a comprehensive review of combinatoric algorithms proposed for learning BN structure from data, describing 61 algorithms including prototypical, well-established and state-of-the-art approaches. The basic approach of each algorithm is described in consistent terms, and the similarities and differences between them highlighted. Methods of evaluating algorithms and their comparative performance are discussed including the consistency of claims made in the literature. Approaches for dealing with data noise in real-world datasets and incorporating expert knowledge into the learning process are also covered.
Bayesian network structure learning with causal effects in the presence of latent variables
May 29, 2020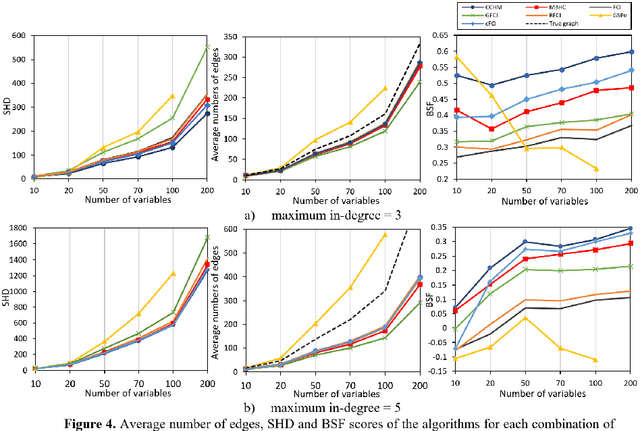
Abstract:Latent variables may lead to spurious relationships that can be misinterpreted as causal relationships. In Bayesian Networks (BNs), this challenge is known as learning under causal insufficiency. Structure learning algorithms that assume causal insufficiency tend to reconstruct the ancestral graph of a BN, where bi-directed edges represent confounding and directed edges represent direct or ancestral relationships. This paper describes a hybrid structure learning algorithm, called CCHM, which combines the constraint-based part of cFCI with hill-climbing score-based learning. The score-based process incorporates Pearl s do-calculus to measure causal effects and orientate edges that would otherwise remain undirected, under the assumption the BN is a linear Structure Equation Model where data follow a multivariate Gaussian distribution. Experiments based on both randomised and well-known networks show that CCHM improves the state-of-the-art in terms of reconstructing the true ancestral graph.
Large-scale empirical validation of Bayesian Network structure learning algorithms with noisy data
May 18, 2020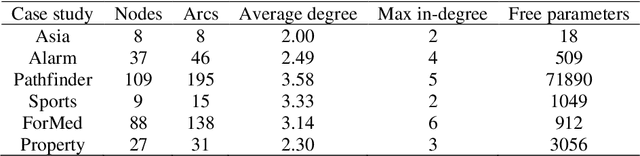
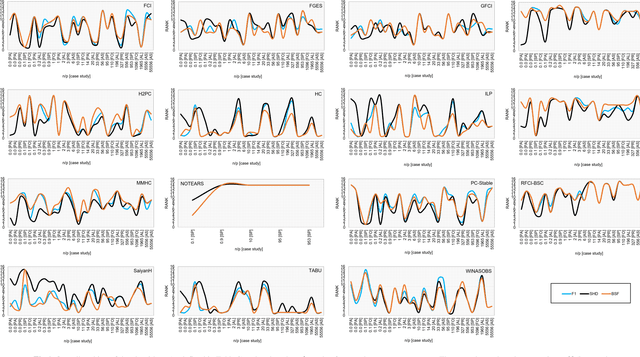
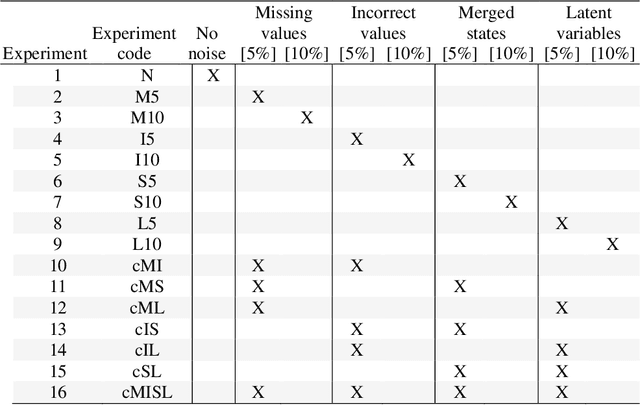
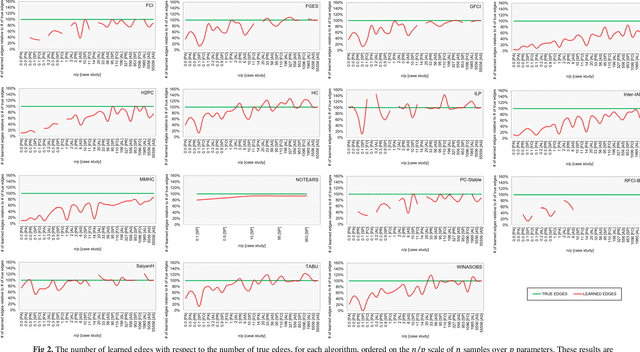
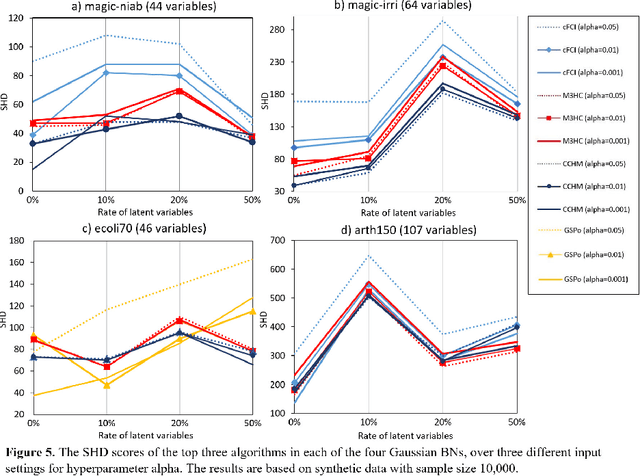
Abstract:Numerous Bayesian Network (BN) structure learning algorithms have been proposed in the literature over the past few decades. Each publication makes an empirical or theoretical case for the algorithm proposed in that publication and results across studies are often inconsistent in their claims about which algorithm is 'best'. This is partly because there is no agreed evaluation approach to determine their effectiveness. Moreover, each algorithm is based on a set of assumptions, such as complete data and causal sufficiency, and tend to be evaluated with data that conforms to these assumptions, however unrealistic these assumptions may be in the real world. As a result, it is widely accepted that synthetic performance overestimates real performance, although to what degree this may happen remains unknown. This paper investigates the performance of 15 structure learning algorithms. We propose a methodology that applies the algorithms to data that incorporates synthetic noise, in an effort to better understand the performance of structure learning algorithms when applied to real data. Each algorithm is tested over multiple case studies, sample sizes, types of noise, and assessed with multiple evaluation criteria. This work involved learning more than 10,000 graphs with a total structure learning runtime of seven months. It provides the first large-scale empirical validation of BN structure learning algorithms under different assumptions of data noise. The results suggest that traditional synthetic performance may overestimate real-world performance by anywhere between 10% and more than 50%. They also show that while score-based learning is generally superior to constraint-based learning, a higher fitting score does not necessarily imply a more accurate causal graph. To facilitate comparisons with future studies, we have made all data, graphs and BN models freely available online.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge