Parallel Sampling for Efficient High-dimensional Bayesian Network Structure Learning

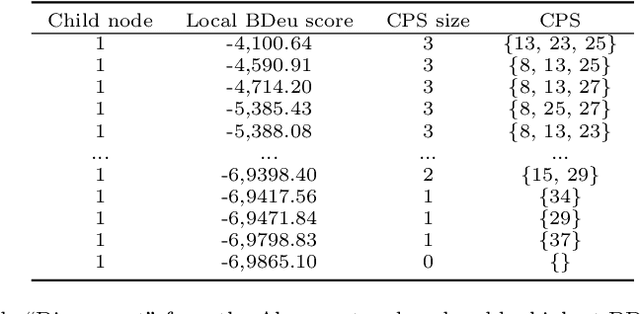
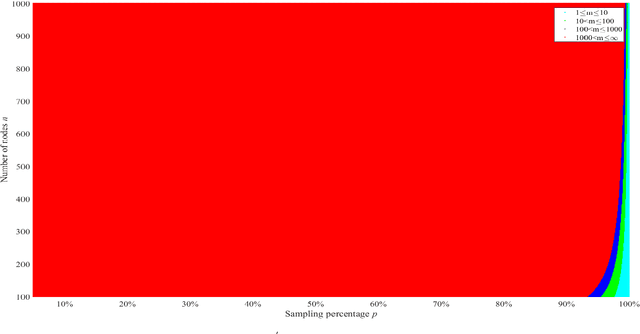
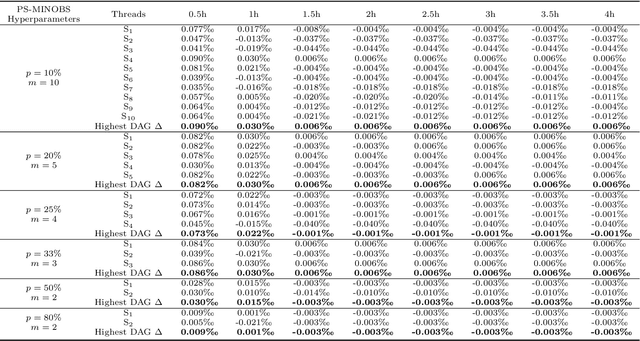
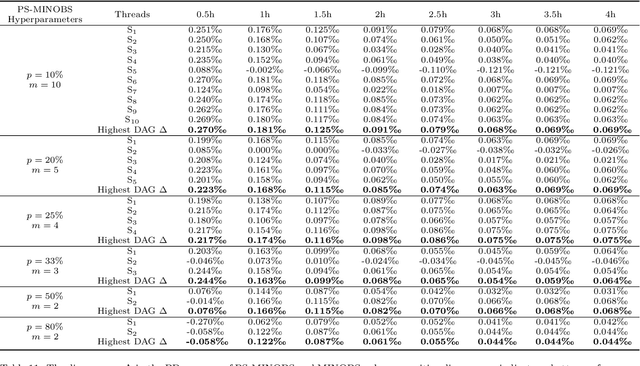
Score-based algorithms that learn the structure of Bayesian networks can be used for both exact and approximate solutions. While approximate learning scales better with the number of variables, it can be computationally expensive in the presence of high dimensional data. This paper describes an approximate algorithm that performs parallel sampling on Candidate Parent Sets (CPSs), and can be viewed as an extension of MINOBS which is a state-of-the-art algorithm for structure learning from high dimensional data. The modified algorithm, which we call Parallel Sampling MINOBS (PS-MINOBS), constructs the graph by sampling CPSs for each variable. Sampling is performed in parallel under the assumption the distribution of CPSs is half-normal when ordered by Bayesian score for each variable. Sampling from a half-normal distribution ensures that the CPSs sampled are likely to be those which produce the higher scores. Empirical results show that, in most cases, the proposed algorithm discovers higher score structures than MINOBS when both algorithms are restricted to the same runtime limit.

Effective and efficient structure learning with pruning and model averaging strategies

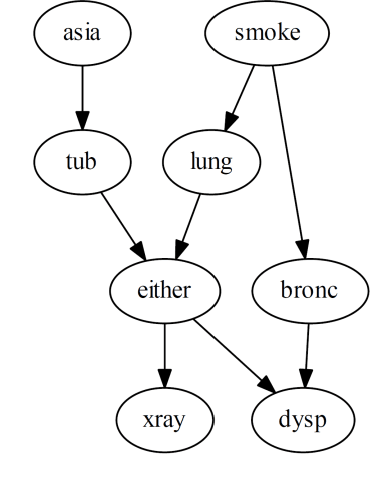
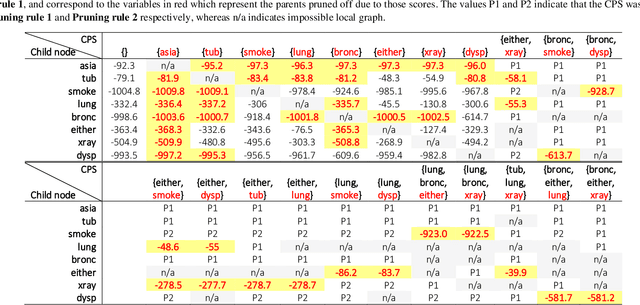
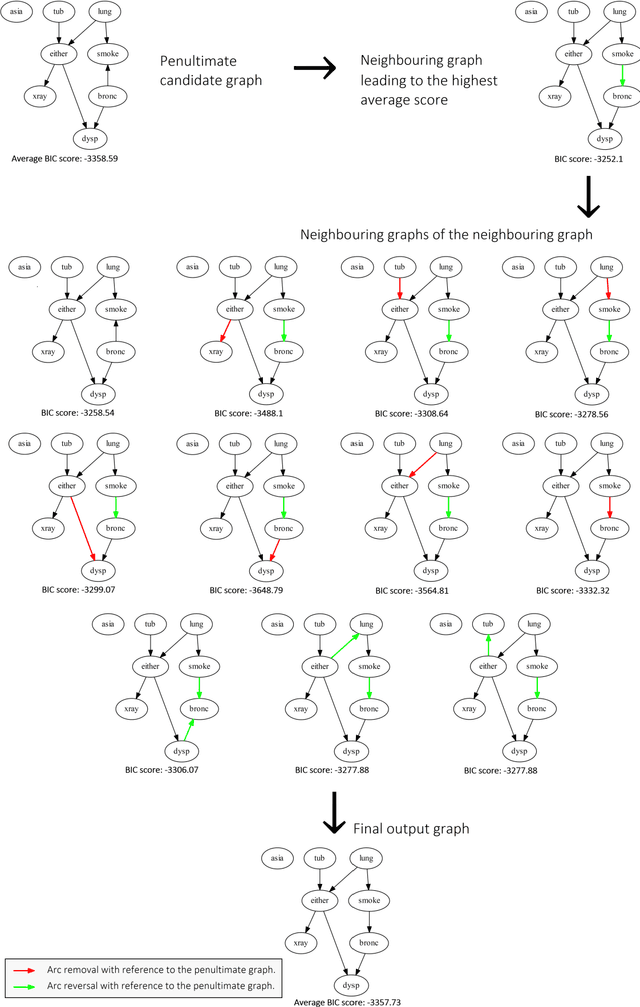
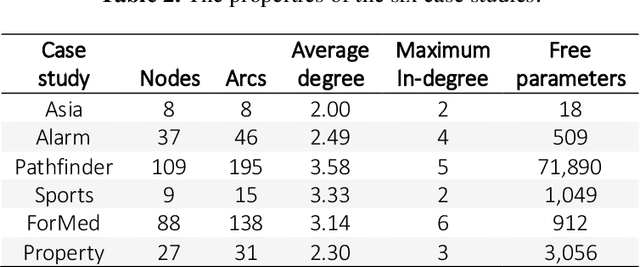
Learning the structure of a Bayesian Network (BN) with score-based solutions involves exploring the search space of possible graphs and moving towards the graph that maximises a given objective function. Some algorithms offer exact solutions that guarantee to return the graph with the highest objective score, while others offer approximate solutions in exchange for reduced computational complexity. This paper describes an approximate BN structure learning algorithm, which we call Model Averaging Hill-Climbing (MAHC), that combines two novel strategies with hill-climbing search. The algorithm starts by pruning the search space of graphs, where the pruning strategy can be viewed as an aggressive version of the pruning strategies that are typically applied to combinatorial optimisation structure learning problems. It then performs model averaging in the hill-climbing search process and moves to the neighbouring graph that maximises the objective function, on average, for that neighbouring graph and over all its valid neighbouring graphs. Comparisons with other algorithms spanning different classes of learning suggest that the combination of aggressive pruning with model averaging is both effective and efficient, particularly in the presence of data noise.

A survey of Bayesian Network structure learning

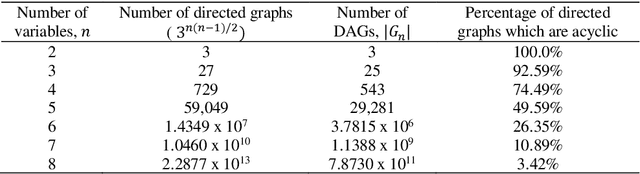
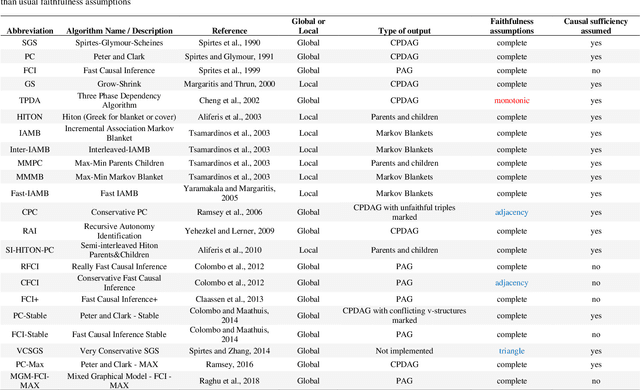
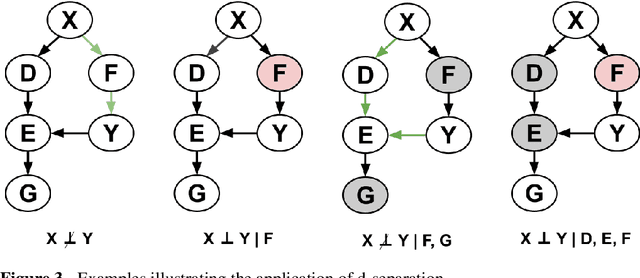
Bayesian Networks (BNs) have become increasingly popular over the last few decades as a tool for reasoning under uncertainty in fields as diverse as medicine, biology, epidemiology, economics and the social sciences. This is especially true in real-world areas where we seek to answer complex questions based on hypothetical evidence to determine actions for intervention. However, determining the graphical structure of a BN remains a major challenge, especially when modelling a problem under causal assumptions. Solutions to this problem include the automated discovery of BN graphs from data, constructing them based on expert knowledge, or a combination of the two. This paper provides a comprehensive review of combinatoric algorithms proposed for learning BN structure from data, describing 61 algorithms including prototypical, well-established and state-of-the-art approaches. The basic approach of each algorithm is described in consistent terms, and the similarities and differences between them highlighted. Methods of evaluating algorithms and their comparative performance are discussed including the consistency of claims made in the literature. Approaches for dealing with data noise in real-world datasets and incorporating expert knowledge into the learning process are also covered.

Information fusion between knowledge and data in Bayesian network structure learning

Bayesian Networks (BNs) have become a powerful technology for reasoning under uncertainty, particularly in areas that require causal assumptions that enable us to simulate the effect of intervention. The graphical structure of these models can be determined by causal knowledge, learnt from data, or a combination of both. While it seems plausible that the best approach in constructing a causal graph involves combining knowledge with machine learning, this approach remains underused in practice. This paper describes and evaluates a set of information fusion methods that have been implemented in the open-source Bayesys structure learning system. The methods enable users to specify pre-existing knowledge and rule-based information that can be obtained from heterogeneous sources, to constrain or guide structure learning. Each method is assessed in terms of structure learning impact, including graphical accuracy, model fitting, complexity and runtime. The results are illustrated both with limited and big data, with application to three BN structure learning algorithms available in Bayesys, and reveal interesting inconsistencies about their effectiveness where the results obtained from graphical measures often contradict those obtained from model fitting measures. While the overall results show that information fusion methods become less effective with big data due to higher learning accuracy rendering knowledge less important, some information fusion methods do perform better with big data. Lastly, amongst the main conclusions is the observation that reduced search space obtained from knowledge constraints does not imply reduced computational complexity, which can happen when the constraints set up a tension between what the data indicate and what the constraints are trying to enforce.

Approximate learning of high dimensional Bayesian network structures via pruning of Candidate Parent Sets

Score-based algorithms that learn Bayesian Network (BN) structures provide solutions ranging from different levels of approximate learning to exact learning. Approximate solutions exist because exact learning is generally not applicable to networks of moderate or higher complexity. In general, approximate solutions tend to sacrifice accuracy for speed, where the aim is to minimise the loss in accuracy and maximise the gain in speed. While some approximate algorithms are optimised to handle thousands of variables, these algorithms may still be unable to learn such high dimensional structures. Some of the most efficient score-based algorithms cast the structure learning problem as a combinatorial optimisation of candidate parent sets. This paper explores a strategy towards pruning the size of candidate parent sets, aimed at high dimensionality problems. The results illustrate how different levels of pruning affect the learning speed in conjunction to the loss in accuracy in terms of model fitting, and show that aggressive pruning may be required to produce approximate solutions for high complexity problems.

Large-scale empirical validation of Bayesian Network structure learning algorithms with noisy data

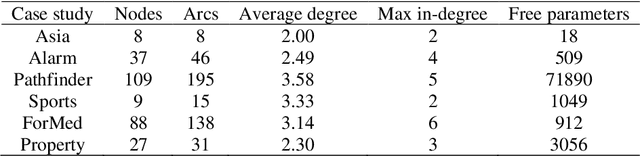
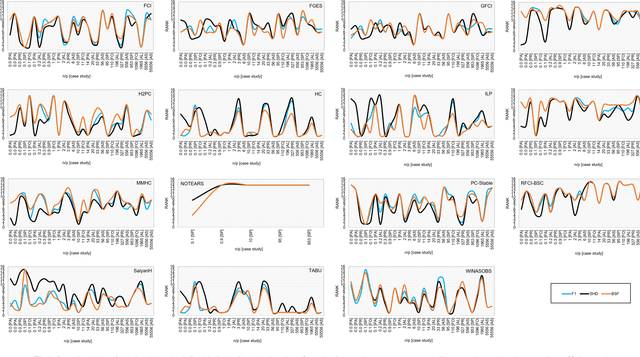
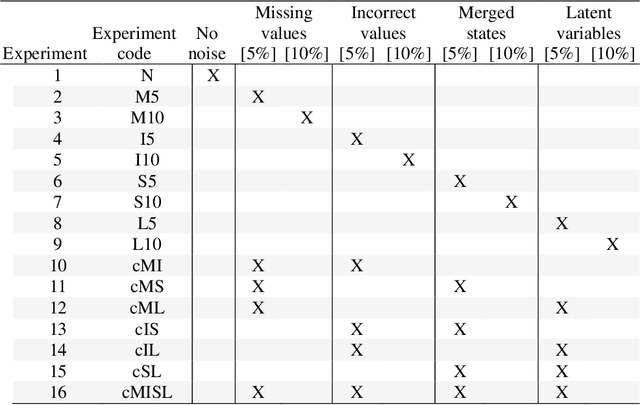
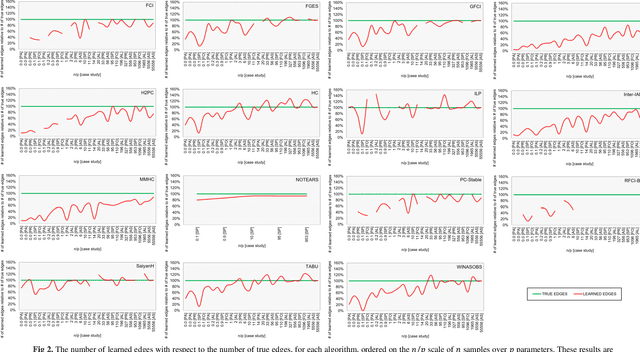
Numerous Bayesian Network (BN) structure learning algorithms have been proposed in the literature over the past few decades. Each publication makes an empirical or theoretical case for the algorithm proposed in that publication and results across studies are often inconsistent in their claims about which algorithm is 'best'. This is partly because there is no agreed evaluation approach to determine their effectiveness. Moreover, each algorithm is based on a set of assumptions, such as complete data and causal sufficiency, and tend to be evaluated with data that conforms to these assumptions, however unrealistic these assumptions may be in the real world. As a result, it is widely accepted that synthetic performance overestimates real performance, although to what degree this may happen remains unknown. This paper investigates the performance of 15 structure learning algorithms. We propose a methodology that applies the algorithms to data that incorporates synthetic noise, in an effort to better understand the performance of structure learning algorithms when applied to real data. Each algorithm is tested over multiple case studies, sample sizes, types of noise, and assessed with multiple evaluation criteria. This work involved learning more than 10,000 graphs with a total structure learning runtime of seven months. It provides the first large-scale empirical validation of BN structure learning algorithms under different assumptions of data noise. The results suggest that traditional synthetic performance may overestimate real-world performance by anywhere between 10% and more than 50%. They also show that while score-based learning is generally superior to constraint-based learning, a higher fitting score does not necessarily imply a more accurate causal graph. To facilitate comparisons with future studies, we have made all data, graphs and BN models freely available online.