RGB to Hyperspectral: Spectral Reconstruction for Enhanced Surgical Imaging

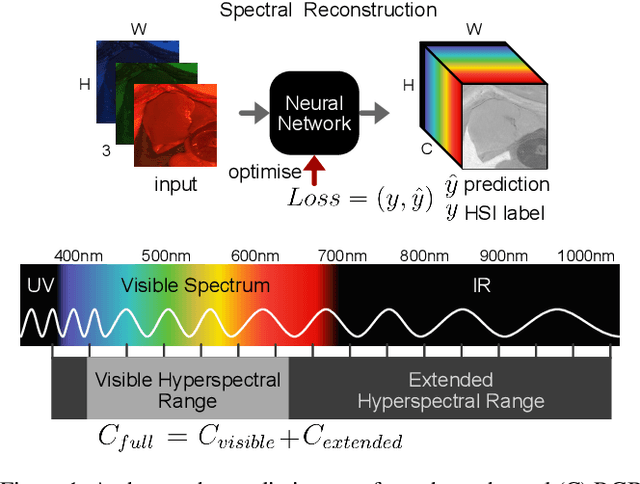
This study investigates the reconstruction of hyperspectral signatures from RGB data to enhance surgical imaging, utilizing the publicly available HeiPorSPECTRAL dataset from porcine surgery and an in-house neurosurgery dataset. Various architectures based on convolutional neural networks (CNNs) and transformer models are evaluated using comprehensive metrics. Transformer models exhibit superior performance in terms of RMSE, SAM, PSNR and SSIM by effectively integrating spatial information to predict accurate spectral profiles, encompassing both visible and extended spectral ranges. Qualitative assessments demonstrate the capability to predict spectral profiles critical for informed surgical decision-making during procedures. Challenges associated with capturing both the visible and extended hyperspectral ranges are highlighted using the MAE, emphasizing the complexities involved. The findings open up the new research direction of hyperspectral reconstruction for surgical applications and clinical use cases in real-time surgical environments.

Sketching the Heat Kernel: Using Gaussian Processes to Embed Data

This paper introduces a novel, non-deterministic method for embedding data in low-dimensional Euclidean space based on computing realizations of a Gaussian process depending on the geometry of the data. This type of embedding first appeared in (Adler et al, 2018) as a theoretical model for a generic manifold in high dimensions. In particular, we take the covariance function of the Gaussian process to be the heat kernel, and computing the embedding amounts to sketching a matrix representing the heat kernel. The Karhunen-Lo\`eve expansion reveals that the straight-line distances in the embedding approximate the diffusion distance in a probabilistic sense, avoiding the need for sharp cutoffs and maintaining some of the smaller-scale structure. Our method demonstrates further advantage in its robustness to outliers. We justify the approach with both theory and experiments.

CA-PCA: Manifold Dimension Estimation, Adapted for Curvature

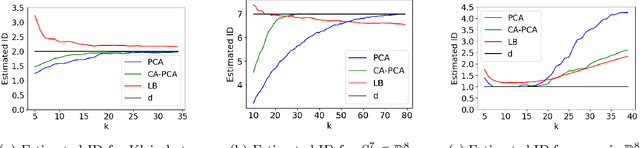
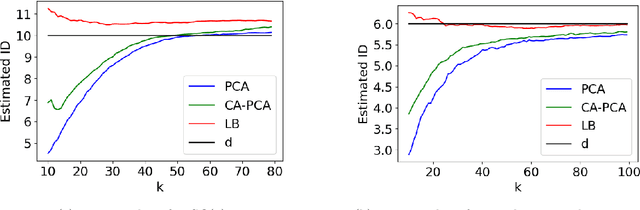
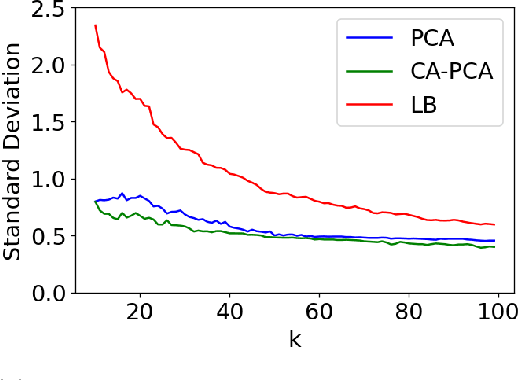
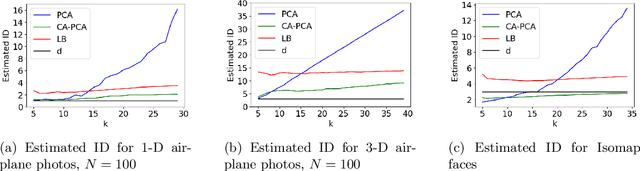
The success of algorithms in the analysis of high-dimensional data is often attributed to the manifold hypothesis, which supposes that this data lie on or near a manifold of much lower dimension. It is often useful to determine or estimate the dimension of this manifold before performing dimension reduction, for instance. Existing methods for dimension estimation are calibrated using a flat unit ball. In this paper, we develop CA-PCA, a version of local PCA based instead on a calibration of a quadratic embedding, acknowledging the curvature of the underlying manifold. Numerous careful experiments show that this adaptation improves the estimator in a wide range of settings.