CA-PCA: Manifold Dimension Estimation, Adapted for Curvature
Paper and Code
Sep 23, 2023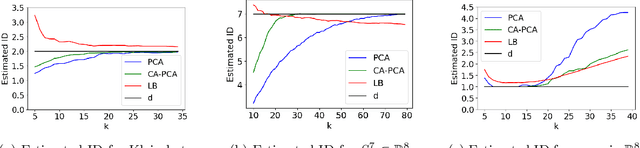
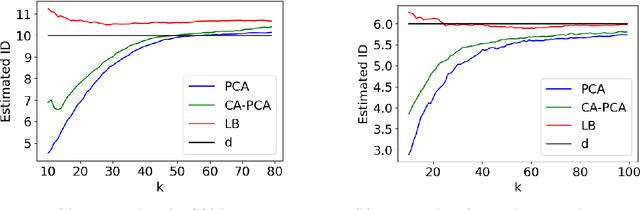
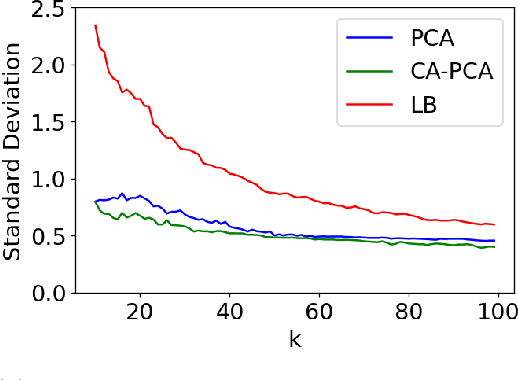
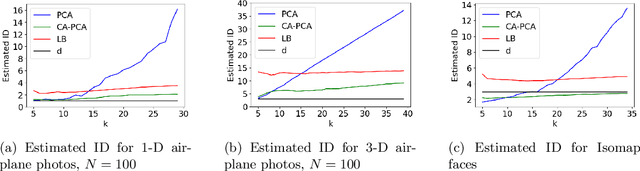
The success of algorithms in the analysis of high-dimensional data is often attributed to the manifold hypothesis, which supposes that this data lie on or near a manifold of much lower dimension. It is often useful to determine or estimate the dimension of this manifold before performing dimension reduction, for instance. Existing methods for dimension estimation are calibrated using a flat unit ball. In this paper, we develop CA-PCA, a version of local PCA based instead on a calibration of a quadratic embedding, acknowledging the curvature of the underlying manifold. Numerous careful experiments show that this adaptation improves the estimator in a wide range of settings.
* 26 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge