OpenKBP-Opt: An international and reproducible evaluation of 76 knowledge-based planning pipelines

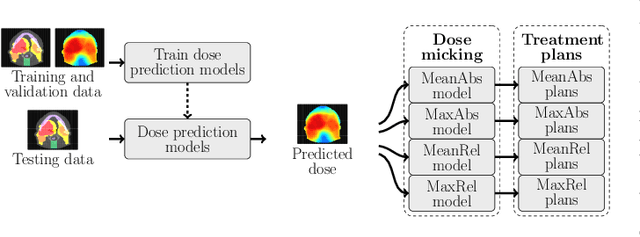
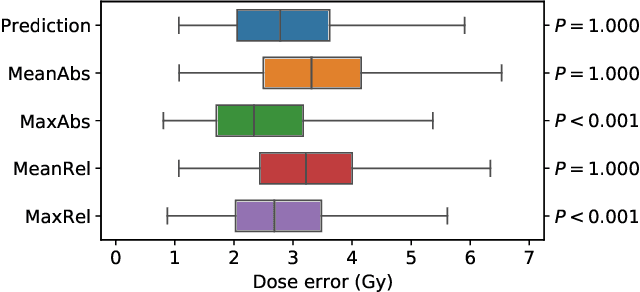
We establish an open framework for developing plan optimization models for knowledge-based planning (KBP) in radiotherapy. Our framework includes reference plans for 100 patients with head-and-neck cancer and high-quality dose predictions from 19 KBP models that were developed by different research groups during the OpenKBP Grand Challenge. The dose predictions were input to four optimization models to form 76 unique KBP pipelines that generated 7600 plans. The predictions and plans were compared to the reference plans via: dose score, which is the average mean absolute voxel-by-voxel difference in dose a model achieved; the deviation in dose-volume histogram (DVH) criterion; and the frequency of clinical planning criteria satisfaction. We also performed a theoretical investigation to justify our dose mimicking models. The range in rank order correlation of the dose score between predictions and their KBP pipelines was 0.50 to 0.62, which indicates that the quality of the predictions is generally positively correlated with the quality of the plans. Additionally, compared to the input predictions, the KBP-generated plans performed significantly better (P<0.05; one-sided Wilcoxon test) on 18 of 23 DVH criteria. Similarly, each optimization model generated plans that satisfied a higher percentage of criteria than the reference plans. Lastly, our theoretical investigation demonstrated that the dose mimicking models generated plans that are also optimal for a conventional planning model. This was the largest international effort to date for evaluating the combination of KBP prediction and optimization models. In the interest of reproducibility, our data and code is freely available at https://github.com/ababier/open-kbp-opt.

OpenKBP: The open-access knowledge-based planning grand challenge

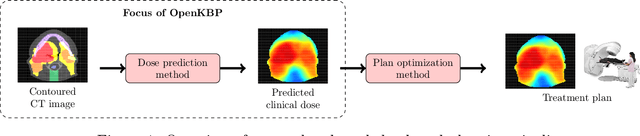
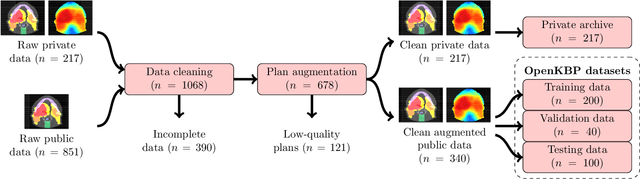
The purpose of this work is to advance fair and consistent comparisons of dose prediction methods for knowledge-based planning (KBP) in radiation therapy research. We hosted OpenKBP, a 2020 AAPM Grand Challenge, and challenged participants to develop the best method for predicting the dose of contoured CT images. The models were evaluated according to two separate scores: (1) dose score, which evaluates the full 3D dose distributions, and (2) dose-volume histogram (DVH) score, which evaluates a set DVH metrics. Participants were given the data of 340 patients who were treated for head-and-neck cancer with radiation therapy. The data was partitioned into training (n=200), validation (n=40), and testing (n=100) datasets. All participants performed training and validation with the corresponding datasets during the validation phase of the Challenge, and we ranked the models in the testing phase based on out-of-sample performance. The Challenge attracted 195 participants from 28 countries, and 73 of those participants formed 44 teams in the validation phase, which received a total of 1750 submissions. The testing phase garnered submissions from 28 teams. On average, over the course of the validation phase, participants improved the dose and DVH scores of their models by a factor of 2.7 and 5.7, respectively. In the testing phase one model achieved significantly better dose and DVH score than the runner-up models. Lastly, many of the top performing teams reported using generalizable techniques (e.g., ensembles) to achieve higher performance than their competition. This is the first competition for knowledge-based planning research, and it helped launch the first platform for comparing KBP prediction methods fairly and consistently. The OpenKBP datasets are available publicly to help benchmark future KBP research, which has also democratized KBP research by making it accessible to everyone.

Blind Detection and Compensation of Camera Lens Geometric Distortions

This paper presents a blind detection and compensation technique for camera lens geometric distortions. The lens distortion introduces higher-order correlations in the frequency domain and in turn it can be detected using higher-order spectral analysis tools without assuming any specific calibration target. The existing blind lens distortion removal method only considered a single-coefficient radial distortion model. In this paper, two coefficients are considered to model approximately the geometric distortion. All the models considered have analytical closed-form inverse formulae.

A Family of Simplified Geometric Distortion Models for Camera Calibration

The commonly used radial distortion model for camera calibration is in fact an assumption or a restriction. In practice, camera distortion could happen in a general geometrical manner that is not limited to the radial sense. This paper proposes a simplified geometrical distortion modeling method by using two different radial distortion functions in the two image axes. A family of simplified geometric distortion models is proposed, which are either simple polynomials or the rational functions of polynomials. Analytical geometric undistortion is possible using two of the distortion functions discussed in this paper and their performance can be improved by applying a piecewise fitting idea. Our experimental results show that the geometrical distortion models always perform better than their radial distortion counterparts. Furthermore, the proposed geometric modeling method is more appropriate for cameras whose distortion is not perfectly radially symmetric around the center of distortion.

Camera Calibration: a USU Implementation

The task of camera calibration is to estimate the intrinsic and extrinsic parameters of a camera model. Though there are some restricted techniques to infer the 3-D information about the scene from uncalibrated cameras, effective camera calibration procedures will open up the possibility of using a wide range of existing algorithms for 3-D reconstruction and recognition. The applications of camera calibration include vision-based metrology, robust visual platooning and visual docking of mobile robots where the depth information is important.

An Analytical Piecewise Radial Distortion Model for Precision Camera Calibration

The common approach to radial distortion is by the means of polynomial approximation, which introduces distortion-specific parameters into the camera model and requires estimation of these distortion parameters. The task of estimating radial distortion is to find a radial distortion model that allows easy undistortion as well as satisfactory accuracy. This paper presents a new piecewise radial distortion model with easy analytical undistortion formula. The motivation for seeking a piecewise radial distortion model is that, when a camera is resulted in a low quality during manufacturing, the nonlinear radial distortion can be complex. Using low order polynomials to approximate the radial distortion might not be precise enough. On the other hand, higher order polynomials suffer from the inverse problem. With the new piecewise radial distortion function, more flexibility is obtained and the radial undistortion can be performed analytically. Experimental results are presented to show that with this new piecewise radial distortion model, better performance is achieved than that using the single function. Furthermore, a comparable performance with the conventional polynomial model using 2 coefficients can also be accomplished.

Rational Radial Distortion Models with Analytical Undistortion Formulae

The common approach to radial distortion is by the means of polynomial approximation, which introduces distortion-specific parameters into the camera model and requires estimation of these distortion parameters. The task of estimating radial distortion is to find a radial distortion model that allows easy undistortion as well as satisfactory accuracy. This paper presents a new class of rational radial distortion models with easy analytical undistortion formulae. Experimental results are presented to show that with this class of rational radial distortion models, satisfactory and comparable accuracy is achieved.

A New Analytical Radial Distortion Model for Camera Calibration

Common approach to radial distortion is by the means of polynomial approximation, which introduces distortion-specific parameters into the camera model and requires estimation of these distortion parameters. The task of estimating radial distortion is to find a radial distortion model that allows easy undistortion as well as satisfactory accuracy. This paper presents a new radial distortion model with an easy analytical undistortion formula, which also belongs to the polynomial approximation category. Experimental results are presented to show that with this radial distortion model, satisfactory accuracy is achieved.

Flexible Camera Calibration Using a New Analytical Radial Undistortion Formula with Application to Mobile Robot Localization

Most algorithms in 3D computer vision rely on the pinhole camera model because of its simplicity, whereas virtually all imaging devices introduce certain amount of nonlinear distortion, where the radial distortion is the most severe part. Common approach to radial distortion is by the means of polynomial approximation, which introduces distortion-specific parameters into the camera model and requires estimation of these distortion parameters. The task of estimating radial distortion is to find a radial distortion model that allows easy undistortion as well as satisfactory accuracy. This paper presents a new radial distortion model with an easy analytical undistortion formula, which also belongs to the polynomial approximation category. Experimental results are presented to show that with this radial distortion model, satisfactory accuracy is achieved. An application of the new radial distortion model is non-iterative yellow line alignment with a calibrated camera on ODIS, a robot built in our CSOIS.