Magic for the Age of Quantized DNNs

Recently, the number of parameters in DNNs has explosively increased, as exemplified by LLMs (Large Language Models), making inference on small-scale computers more difficult. Model compression technology is, therefore, essential for integration into products. In this paper, we propose a method of quantization-aware training. We introduce a novel normalization (Layer-Batch Normalization) that is independent of the mini-batch size and does not require any additional computation cost during inference. Then, we quantize the weights by the scaled round-clip function with the weight standardization. We also quantize activation functions using the same function and apply surrogate gradients to train the model with both quantized weights and the quantized activation functions. We call this method Magic for the age of Quantised DNNs (MaQD). Experimental results show that our quantization method can be achieved with minimal accuracy degradation.

Convergences for Minimax Optimization Problems over Infinite-Dimensional Spaces Towards Stability in Adversarial Training

Training neural networks that require adversarial optimization, such as generative adversarial networks (GANs) and unsupervised domain adaptations (UDAs), suffers from instability. This instability problem comes from the difficulty of the minimax optimization, and there have been various approaches in GANs and UDAs to overcome this problem. In this study, we tackle this problem theoretically through a functional analysis. Specifically, we show the convergence property of the minimax problem by the gradient descent over the infinite-dimensional spaces of continuous functions and probability measures under certain conditions. Using this setting, we can discuss GANs and UDAs comprehensively, which have been studied independently. In addition, we show that the conditions necessary for the convergence property are interpreted as stabilization techniques of adversarial training such as the spectral normalization and the gradient penalty.

Spiking Synaptic Penalty: Appropriate Penalty Term for Energy-Efficient Spiking Neural Networks

Spiking neural networks (SNNs) are energy-efficient neural networks because of their spiking nature. However, as the spike firing rate of SNNs increases, the energy consumption does as well, and thus, the advantage of SNNs diminishes. Here, we tackle this problem by introducing a novel penalty term for the spiking activity into the objective function in the training phase. Our method is designed so as to optimize the energy consumption metric directly without modifying the network architecture. Therefore, the proposed method can reduce the energy consumption more than other methods while maintaining the accuracy. We conducted experiments for image classification tasks, and the results indicate the effectiveness of the proposed method, which mitigates the dilemma of the energy--accuracy trade-off.

Variational Inference with Gaussian Mixture by Entropy Approximation

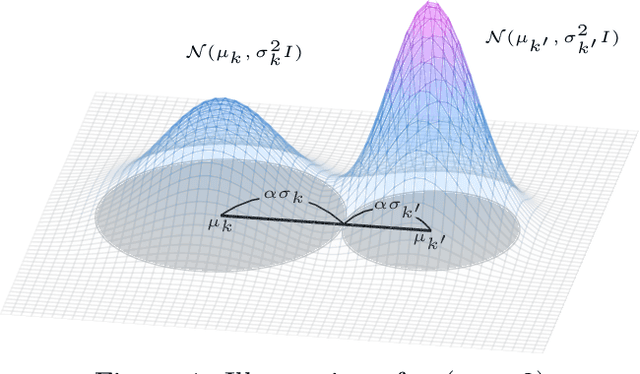
Variational inference is a technique for approximating intractable posterior distributions in order to quantify the uncertainty of machine learning. Although the unimodal Gaussian distribution is usually chosen as a parametric distribution, it hardly approximates the multimodality. In this paper, we employ the Gaussian mixture distribution as a parametric distribution. A main difficulty of variational inference with the Gaussian mixture is how to approximate the entropy of the Gaussian mixture. We approximate the entropy of the Gaussian mixture as the sum of the entropy of the unimodal Gaussian, which can be analytically calculated. In addition, we theoretically analyze the approximation error between the true entropy and approximated one in order to reveal when our approximation works well. Specifically, the approximation error is controlled by the ratios of the distances between the means to the sum of the variances of the Gaussian mixture, and it converges to zero when the ratios go to infinity. This situation seems to be more likely to occur in higher dimensional weight spaces because of the curse of dimensionality. Therefore, our result guarantees that our approximation works well, for example, in neural networks that assume a large number of weights.

S$^2$NN: Time Step Reduction of Spiking Surrogate Gradients for Training Energy Efficient Single-Step Neural Networks

As the scales of neural networks increase, techniques that enable them to run with low computational cost and energy efficiency are required. From such demands, various efficient neural network paradigms, such as spiking neural networks (SNNs) or binary neural networks (BNNs), have been proposed. However, they have sticky drawbacks, such as degraded inference accuracy and latency. To solve these problems, we propose a single-step neural network (S$^2$NN), an energy-efficient neural network with low computational cost and high precision. The proposed S$^2$NN processes the information between hidden layers by spikes as SNNs. Nevertheless, it has no temporal dimension so that there is no latency within training and inference phases as BNNs. Thus, the proposed S$^2$NN has a lower computational cost than SNNs that require time-series processing. However, S$^2$NN cannot adopt na\"{i}ve backpropagation algorithms due to the non-differentiability nature of spikes. We deduce a suitable neuron model by reducing the surrogate gradient for multi-time step SNNs to a single-time step. We experimentally demonstrated that the obtained neuron model enables S$^2$NN to train more accurately and energy-efficiently than existing neuron models for SNNs and BNNs. We also showed that the proposed S$^2$NN could achieve comparable accuracy to full-precision networks while being highly energy-efficient.

Spectral Pruning for Recurrent Neural Networks

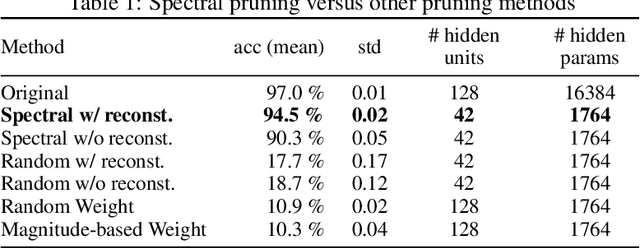
Pruning techniques for neural networks with a recurrent architecture, such as the recurrent neural network (RNN), are strongly desired for their application to edge-computing devices. However, the recurrent architecture is generally not robust to pruning because even small pruning causes accumulation error and the total error increases significantly over time. In this paper, we propose an appropriate pruning algorithm for RNNs inspired by "spectral pruning", and provide the generalization error bounds for compressed RNNs. We also provide numerical experiments to demonstrate our theoretical results and show the effectiveness of our pruning method compared with existing methods.