Enhancing AI System Resiliency: Formulation and Guarantee for LSTM Resilience Based on Control Theory

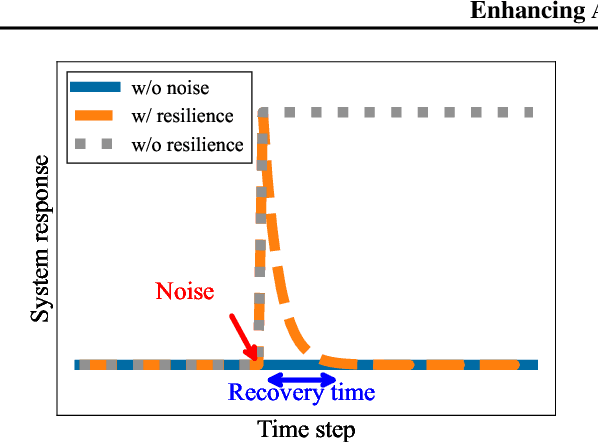
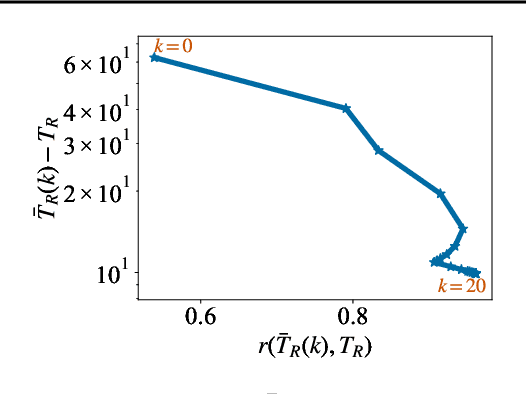
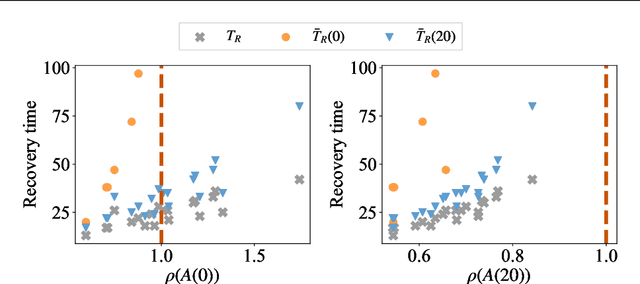
This research proposes methods for formulating and guaranteeing the resilience of long short-term memory (LSTM) networks, which can serve as a key technology in AI system quality assurance. We introduce a novel methodology applying incremental input-to-state stability ($\delta$ISS) to mathematically define and evaluate the resilience of LSTM against input perturbations. Key achievements include the development of a data-independent evaluation method and the demonstration of resilience control through adjustments to training parameters. This research presents concrete solutions to AI quality assurance from a control theory perspective, which can advance AI applications in control systems.

Spike Accumulation Forwarding for Effective Training of Spiking Neural Networks

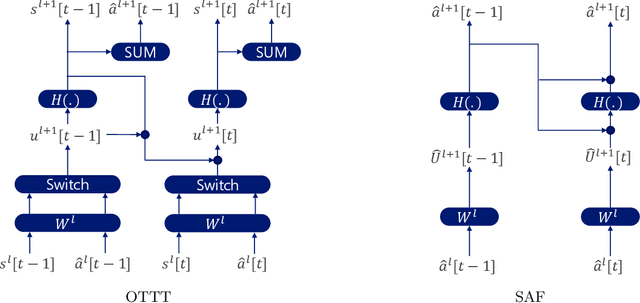
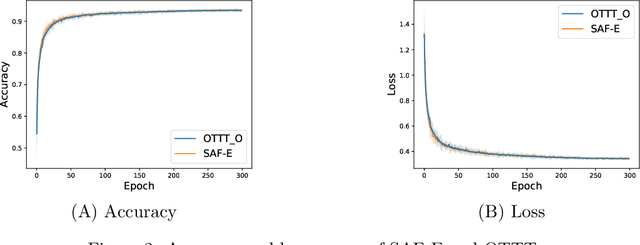
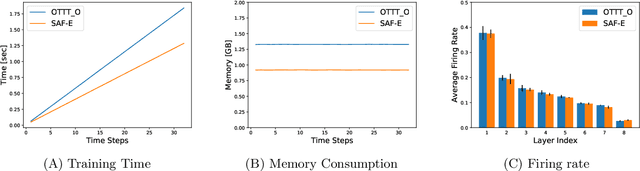
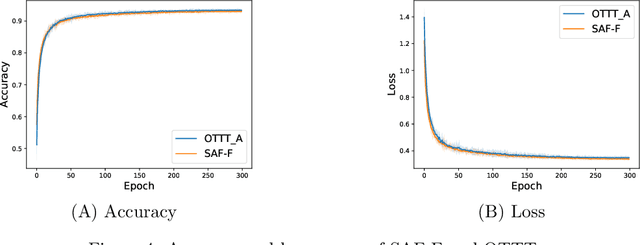
In this article, we propose a new paradigm for training spiking neural networks (SNNs), spike accumulation forwarding (SAF). It is known that SNNs are energy-efficient but difficult to train. Consequently, many researchers have proposed various methods to solve this problem, among which online training through time (OTTT) is a method that allows inferring at each time step while suppressing the memory cost. However, to compute efficiently on GPUs, OTTT requires operations with spike trains and weighted summation of spike trains during forwarding. In addition, OTTT has shown a relationship with the Spike Representation, an alternative training method, though theoretical agreement with Spike Representation has yet to be proven. Our proposed method can solve these problems; namely, SAF can halve the number of operations during the forward process, and it can be theoretically proven that SAF is consistent with the Spike Representation and OTTT, respectively. Furthermore, we confirmed the above contents through experiments and showed that it is possible to reduce memory and training time while maintaining accuracy.

Variational Inference with Gaussian Mixture by Entropy Approximation

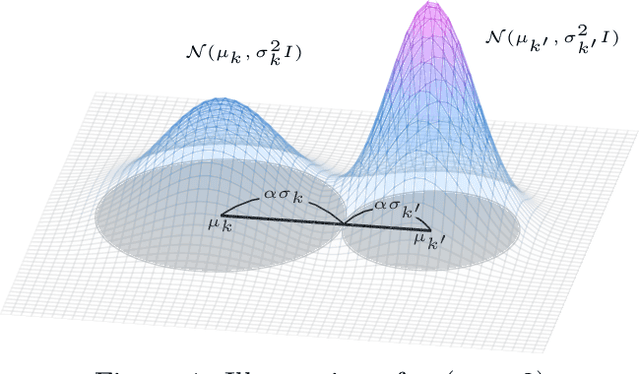
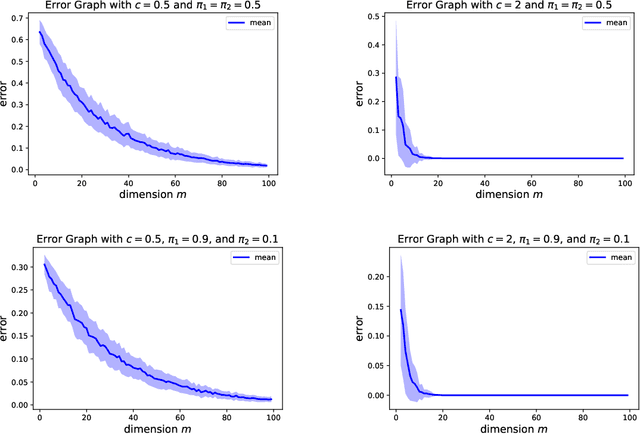
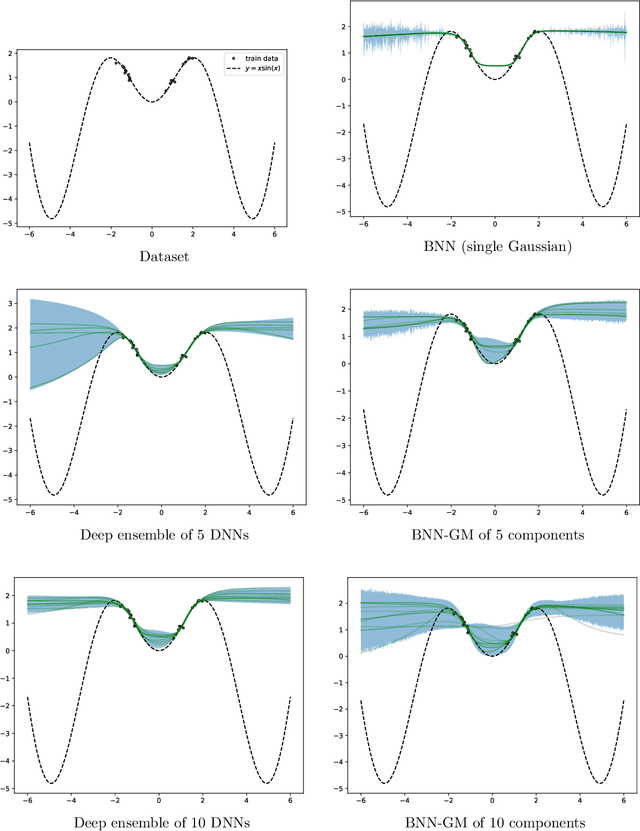
Variational inference is a technique for approximating intractable posterior distributions in order to quantify the uncertainty of machine learning. Although the unimodal Gaussian distribution is usually chosen as a parametric distribution, it hardly approximates the multimodality. In this paper, we employ the Gaussian mixture distribution as a parametric distribution. A main difficulty of variational inference with the Gaussian mixture is how to approximate the entropy of the Gaussian mixture. We approximate the entropy of the Gaussian mixture as the sum of the entropy of the unimodal Gaussian, which can be analytically calculated. In addition, we theoretically analyze the approximation error between the true entropy and approximated one in order to reveal when our approximation works well. Specifically, the approximation error is controlled by the ratios of the distances between the means to the sum of the variances of the Gaussian mixture, and it converges to zero when the ratios go to infinity. This situation seems to be more likely to occur in higher dimensional weight spaces because of the curse of dimensionality. Therefore, our result guarantees that our approximation works well, for example, in neural networks that assume a large number of weights.

Spectral Pruning for Recurrent Neural Networks

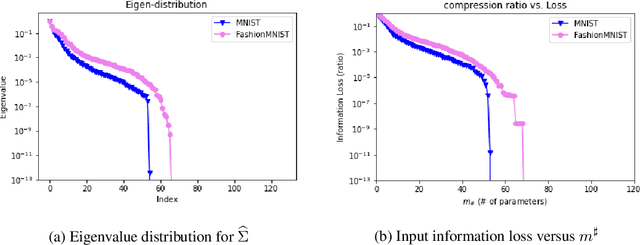
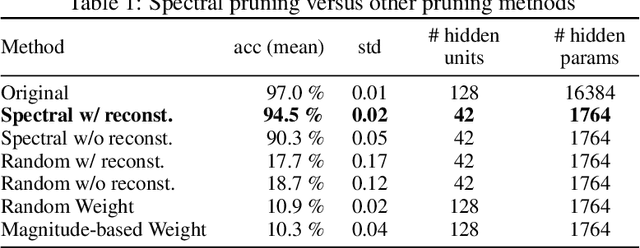
Pruning techniques for neural networks with a recurrent architecture, such as the recurrent neural network (RNN), are strongly desired for their application to edge-computing devices. However, the recurrent architecture is generally not robust to pruning because even small pruning causes accumulation error and the total error increases significantly over time. In this paper, we propose an appropriate pruning algorithm for RNNs inspired by "spectral pruning", and provide the generalization error bounds for compressed RNNs. We also provide numerical experiments to demonstrate our theoretical results and show the effectiveness of our pruning method compared with existing methods.