Quantitative Approximation for Neural Operators in Nonlinear Parabolic Equations

Neural operators serve as universal approximators for general continuous operators. In this paper, we derive the approximation rate of solution operators for the nonlinear parabolic partial differential equations (PDEs), contributing to the quantitative approximation theorem for solution operators of nonlinear PDEs. Our results show that neural operators can efficiently approximate these solution operators without the exponential growth in model complexity, thus strengthening the theoretical foundation of neural operators. A key insight in our proof is to transfer PDEs into the corresponding integral equations via Duahamel's principle, and to leverage the similarity between neural operators and Picard's iteration, a classical algorithm for solving PDEs. This approach is potentially generalizable beyond parabolic PDEs to a range of other equations, including the Navier-Stokes equation, nonlinear Schr\"odinger equations and nonlinear wave equations, which can be solved by Picard's iteration.

Variational Inference with Gaussian Mixture by Entropy Approximation

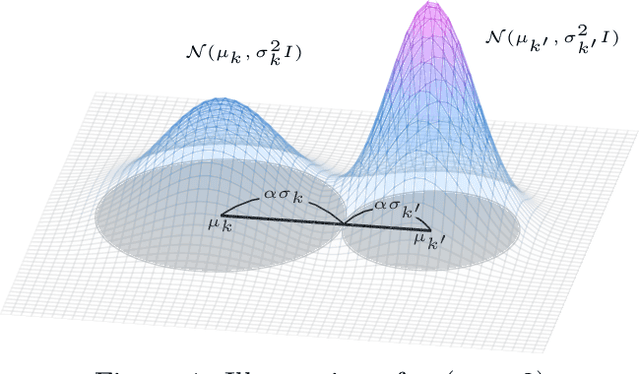
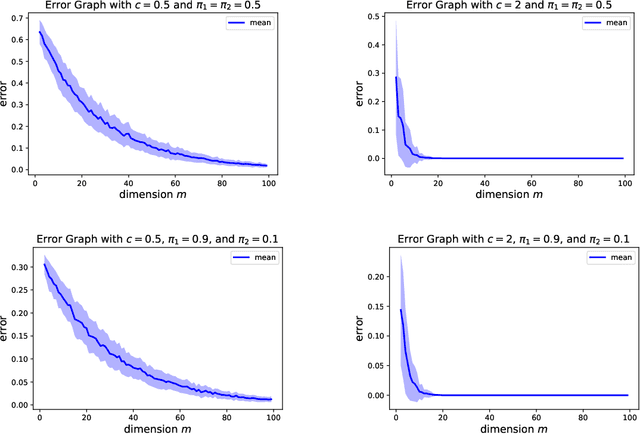
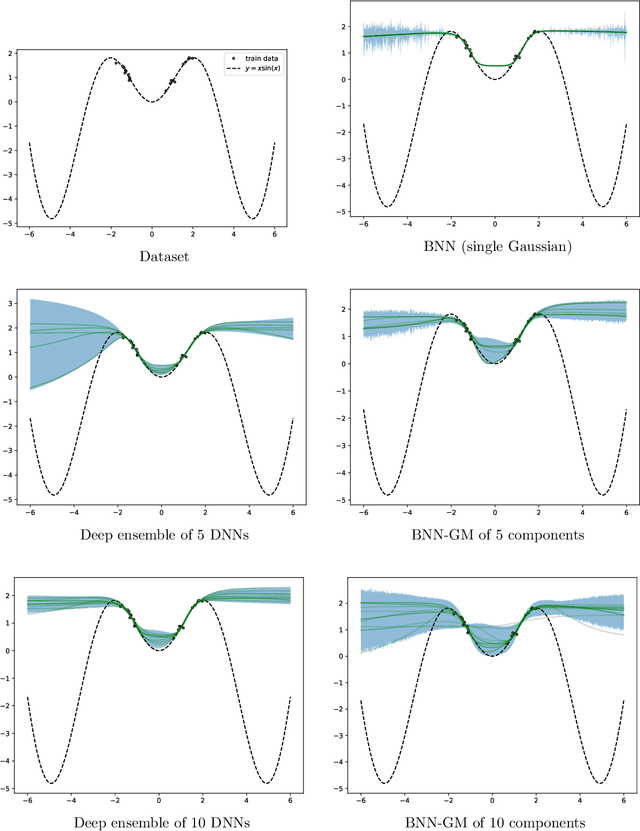
Variational inference is a technique for approximating intractable posterior distributions in order to quantify the uncertainty of machine learning. Although the unimodal Gaussian distribution is usually chosen as a parametric distribution, it hardly approximates the multimodality. In this paper, we employ the Gaussian mixture distribution as a parametric distribution. A main difficulty of variational inference with the Gaussian mixture is how to approximate the entropy of the Gaussian mixture. We approximate the entropy of the Gaussian mixture as the sum of the entropy of the unimodal Gaussian, which can be analytically calculated. In addition, we theoretically analyze the approximation error between the true entropy and approximated one in order to reveal when our approximation works well. Specifically, the approximation error is controlled by the ratios of the distances between the means to the sum of the variances of the Gaussian mixture, and it converges to zero when the ratios go to infinity. This situation seems to be more likely to occur in higher dimensional weight spaces because of the curse of dimensionality. Therefore, our result guarantees that our approximation works well, for example, in neural networks that assume a large number of weights.

Spectral Pruning for Recurrent Neural Networks

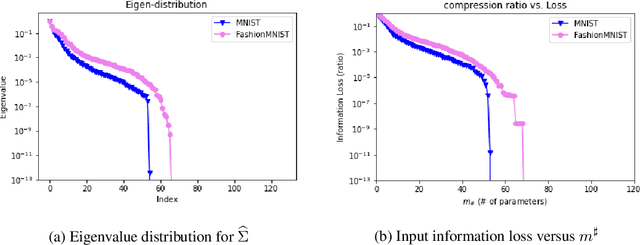
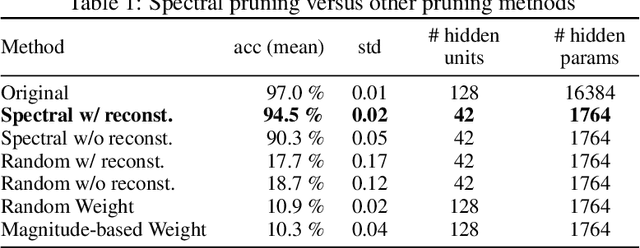
Pruning techniques for neural networks with a recurrent architecture, such as the recurrent neural network (RNN), are strongly desired for their application to edge-computing devices. However, the recurrent architecture is generally not robust to pruning because even small pruning causes accumulation error and the total error increases significantly over time. In this paper, we propose an appropriate pruning algorithm for RNNs inspired by "spectral pruning", and provide the generalization error bounds for compressed RNNs. We also provide numerical experiments to demonstrate our theoretical results and show the effectiveness of our pruning method compared with existing methods.